题目内容
如图1,在 中,
中, ,
, ,
, ,另有一等腰梯形
,另有一等腰梯形 (
( )的底边
)的底边 与
与 重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.

1.直接写出△AGF与△ABC的面积的比值;
2.操作:固定 ,将等腰梯形
,将等腰梯形 以每秒1个单位的速度沿
以每秒1个单位的速度沿 方向向右运动,直到点
方向向右运动,直到点 与点
与点 重合时停止.设运动时间为
重合时停止.设运动时间为 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为 (如图2).
(如图2).

①探究1:在运动过程中,四边形 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时 的值;若不能,请说明理由.
的值;若不能,请说明理由.
②探究2:设在运动过程中 与等腰梯形
与等腰梯形 重叠部分的面积为
重叠部分的面积为 ,求
,求 与
与 的函数关系式.
的函数关系式.
【答案】
1.△AGF与△ABC的面积比是1:4.
2.①能为菱形. (1分)
由于FC∥ ,CE∥
,CE∥ ,
,
 四边形
四边形 是平行四边形. (1分)
是平行四边形. (1分)
当 时,四边形
时,四边形 为菱形,( 1分)
为菱形,( 1分)
此时可求得 .
.
 当
当 秒时,四边形
秒时,四边形 为 (1分)
为 (1分)
②分两种情况:
①当 时,
时,
如图3过点 作
作 于
于 .
.

 ,
, ,
, ,
, 为
为 中点,
中点,
 .
.
又 分别为
分别为 的中点,
的中点,
 . ( 1分)
. ( 1分)

 等腰梯形
等腰梯形 的面积为6.
的面积为6.
 ,
, .
.
 重叠部分的面积为:
重叠部分的面积为: . ( 1分)
. ( 1分)
 当
当 时,
时, 与
与 的函数关系式为
的函数关系式为 .
( 1分)
.
( 1分)
②当 时,
时,
设 与
与 交于点
交于点 ,则
,则 .
. ,
, ,
,
作 于
于 ,则.
,则. ( 1分)
( 1分)
 重叠部分的面积为:
重叠部分的面积为:
 .
.
综上,当 时,
时, 与
与 的函数关系式为
的函数关系式为 ;当
;当 时,
时, ( 1分)
( 1分)
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, ,
, ,
, ,另有一等腰梯形
,另有一等腰梯形 (
( )的底边
)的底边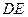 与
与 重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
 ,将等腰梯形
,将等腰梯形 与点
与点 重合时停止.设运动时间为
重合时停止.设运动时间为 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为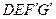 (如图2).
(如图2).
 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时 ,求
,求 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。
 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 , 则
则 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。
 ,则
,则 的值是 (用含
的值是 (用含 的代数式表示).
的代数式表示).

 中,
中, 是
是 与
与 的平分线
的平分线 和
和 的交点,分析发现
的交点,分析发现 ,理由如下: ∵
,理由如下: ∵


 的平分线
的平分线 与
与 有怎样的关系?请说明理由.
有怎样的关系?请说明理由. 与外角
与外角 的平分线
的平分线 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。
 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是
,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是
,  则
则 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。
 ,则
,则 的值是
(用含
的值是
(用含 的代数式表示).
的代数式表示).
 中,点
中,点 是
是 边的中点,点
边的中点,点 在
在 边上(不与端点重合).
边上(不与端点重合). 
 ,且
,且 ,求证:
,求证: 是
是 ,则结论“
,则结论“