Question

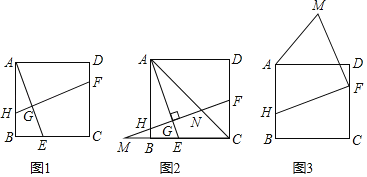
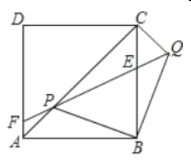
【题目】如图，正方形、等腰的顶点在对角线上(点与、不重合)，与交于，延长线与交于点，连接.

(1)求证：.

(2)求证：

(3)若，求的值.

Answer 1

【答案】(1)证明见解析；(2)证明见解析；(3).

【解析】

（1）证出∠ABP=∠CBQ，由SAS证明△ABP≌△CBQ可得结论；
（2）根据正方形的性质和全等三角形的性质得到，∠APF=∠ABP，可证明△APF∽△ABP，再根据相似三角形的性质即可求解；
（3）根据全等三角形的性质得到∠BCQ=∠BAC=45°，可得∠PCQ=90°，根据三角函数和已知条件得到，由（2）可得，等量代换可得∠CBQ=∠CPQ即可求解．

(1)∵是正方形，

∴，，

∵是等腰三角形，

∴，，

∴，

∴，

∴；

(2)∵是正方形，

∴，，

∵是等腰三角形，

∴，

∵，

∵，

∴，

∴，

∴，

∴，

∴，

；

(3)由(1)得，，，

∴，

由(2)，

∴，

∵，

∴，

在中，

，

∴