题目内容
1.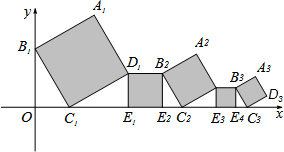 如图,在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3,…,按图示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3,…,在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,…,则正方形A2016B2016C2016D2016的边长是( )
如图,在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3,…,按图示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3,…,在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,…,则正方形A2016B2016C2016D2016的边长是( )| A. | ($\frac{1}{2}$)2015 | B. | ($\frac{1}{2}$)2016 | C. | ($\frac{\sqrt{3}}{3}$)2016 | D. | ($\frac{\sqrt{3}}{3}$)2015 |
分析 利用正方形的性质结合锐角三角函数关系得出正方形的边长,进而得出变化规律即可得出答案.
解答 解:如图所示:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…
∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,
∴D1E1=C1D1sin30°=$\frac{1}{2}$,则B2C2=($\frac{\sqrt{3}}{3}$)1,
同理可得:B3C3=$\frac{1}{3}$=($\frac{\sqrt{3}}{3}$)2,
故正方形AnBnCnDn的边长是:($\frac{\sqrt{3}}{3}$)n-1.
则正方形A2016B2016C2016D2016的边长是:($\frac{\sqrt{3}}{3}$)2015.
故选:D.
点评 此题主要考查了正方形的性质、锐角三角函数;熟练掌握正方形的性质,得出正方形的边长变化规律是解题关键.

练习册系列答案
相关题目
13. 如图,身高为1.6m的吴格霆想测量学校旗杆的高度,当她站在C处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是( )
如图,身高为1.6m的吴格霆想测量学校旗杆的高度,当她站在C处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是( )
 如图,身高为1.6m的吴格霆想测量学校旗杆的高度,当她站在C处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是( )
如图,身高为1.6m的吴格霆想测量学校旗杆的高度,当她站在C处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是( )| A. | 6.4m | B. | 7.0m | C. | 8.0m | D. | 9.0m |
10.下面是一个被墨水污染过的方程:4x-$\frac{1}{2}$=3x+ ,答案显示此方程的解是x=-1,被墨水遮盖的是一个常数,则这个常数是( )
,答案显示此方程的解是x=-1,被墨水遮盖的是一个常数,则这个常数是( )
 ,答案显示此方程的解是x=-1,被墨水遮盖的是一个常数,则这个常数是( )
,答案显示此方程的解是x=-1,被墨水遮盖的是一个常数,则这个常数是( )| A. | 1 | B. | -1 | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{2}$ |
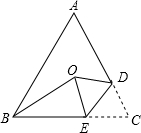 如图,在等腰△ABC中,AB=AC,将△ABC沿DE折叠,使底角顶点C落在三角形三边的垂直平分线的交点O处,若BE=BO,则∠ABC=63度.
如图,在等腰△ABC中,AB=AC,将△ABC沿DE折叠,使底角顶点C落在三角形三边的垂直平分线的交点O处,若BE=BO,则∠ABC=63度.