题目内容
已知，如图，OA，OB，OC是⊙O的半径， |
| AC |
|
| AB |
考点：圆心角、弧、弦的关系,全等三角形的判定与性质
专题：证明题
分析：由OA，OB，OC是⊙O的半径，
=
，根据弧与圆心角的关系，可得∠AOC=∠BOC，又由点M，N分别是OA，OB的中点，可得OM=ON，继而可证得△OCM≌△OCN，则可得MC=NC．
 |
| AC |
|
| AB |
解答：证明：∵OA，OB，OC是⊙O的半径，
=
，
∴∠AOC=∠BOC，
∵点M，N分别是OA，OB的中点，OA=OB，
∴OM=ON，
在△OCM和△OCN中，
，
∴△OCM≌△OCN（SAS），
∴MC=NC．
|
| AC |
|
| AB |
∴∠AOC=∠BOC，
∵点M，N分别是OA，OB的中点，OA=OB，
∴OM=ON，
在△OCM和△OCN中，
|
∴△OCM≌△OCN（SAS），
∴MC=NC．
点评：此题考查了弧与圆心角的关系以及全等三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
整理一批图书，由一个人做要40h完成，现计划有一部分人先做4h，然后增加2人与他们一起做8h，完成这项工作，假设这些人的工作效率相同，具体应先安排多少人工作？如果设安排x人先做4h，下列四个方程中正确的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列计算错误的是（ ）
| A、（-3）2=6 | ||||||
B、-
| ||||||
| C、0-（-1）=1 | ||||||
| D、|-3|=3 |
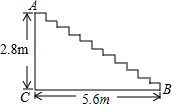某商场重新装修后，准备在大厅的主楼梯上铺设一种红色的地毯，已知这种地毯的批发价为每平方米40元，已知主楼梯道的宽为3米，其侧面如图，则买地毯至少需要多少元？