题目内容
6.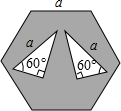 如图,在边长为a的正六边形内有两个小三角形,相关数据如图所示.若图中阴影部分的面积为S1,两个空白三角形的面积为S2.则$\frac{S_1}{S_2}$=( )
如图,在边长为a的正六边形内有两个小三角形,相关数据如图所示.若图中阴影部分的面积为S1,两个空白三角形的面积为S2.则$\frac{S_1}{S_2}$=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 先求得两个三角形的面积,再求出正六边形的面积,求比值即可.
解答  解:如图,
解:如图,
∵三角形的斜边长为a,
∴两条直角边长为$\frac{1}{2}$a,$\frac{\sqrt{3}}{2}$a,
∴S2=$\frac{1}{2}$a•$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{4}$a2,
∵AB=a,
∴OC=$\frac{\sqrt{3}}{2}$a,
∴S正六边形=6×$\frac{1}{2}$a•$\frac{\sqrt{3}}{2}$a=$\frac{3\sqrt{3}}{2}$a2,
∴S1=S正六边形-S空白=$\frac{3\sqrt{3}}{2}$a2-$\frac{\sqrt{3}}{4}$a2=$\frac{5\sqrt{3}}{4}$a2,
∴$\frac{S_1}{S_2}$=$\frac{\frac{5\sqrt{3}}{4}{a}^{2}}{\frac{\sqrt{3}}{4}{a}^{2}}$=5.
故选C.
点评 本题考查了正多边形和圆,正六边形的边长等于半径,面积可以分成六个等边三角形的面积来计算.

练习册系列答案
相关题目
17.下列调查方式合适的是( )
| A. | 为了了解市民对电影《南京》的感受,小华在某校随机采访了8名初三学生 | |
| B. | 为了了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查 | |
| C. | 为了了解全国青少年儿童的睡眠时间,统计人员采用了普查的方式 | |
| D. | 为了了解“嫦娥一号”卫星零部件的状况,检测人员采用了普查的方式 |
17.下列计算正确的是( )
| A. | x-2x=x | B. | x6÷x3=x2 | C. | (-x2)3=-x6 | D. | (x+y)2=x2+y2 |
10.若x=2是关于x的一元二次方程x2+x+m=0的一个根,则m是( )
| A. | 6 | B. | 3 | C. | -6 | D. | -3 |
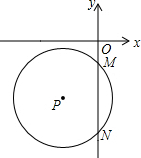 如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=-2x+m图象过点P,则m=-15.
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=-2x+m图象过点P,则m=-15.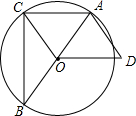 如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.
如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.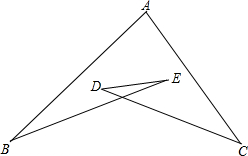 如图,∠A+∠B+∠C+∠D+∠E=180°.
如图,∠A+∠B+∠C+∠D+∠E=180°. 实数a在数轴上的位置如图所示,化简|a-1|+a=1.
实数a在数轴上的位置如图所示,化简|a-1|+a=1.