题目内容
在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
(1)f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
(2)g(m,n)=(﹣m,﹣n),如g (2,1)=(﹣2,﹣1)
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]=
(3,2) .
解:∵f(﹣3,2)=(﹣3,﹣2),
∴g[f(﹣3,2)]=g(﹣3,﹣2)=(3,2),

练习册系列答案
相关题目
下列计算正确的是( )
|
| A. | (﹣1)﹣1=1 | B. | (﹣1)0=0 | C. | |﹣1|=﹣1 | D. | ﹣(﹣1)2=﹣1 |
某班第一组12名同学在“爱心捐款”活动中,捐款情况统计如下表,则捐款数组成的一组数据中,中位数与众数分别是( )
| 捐款(元) | 10 | 15 | 20 | 50 |
| 人数 | 1 | 5 | 4 | 2 |
|
| A. | 15,15 | B. | 17.5,15 | C. | 20,20 | D. | 15,20 |
 B.
B.  C.
C.  D.
D. 
 的自变量x的取值范围是
的自变量x的取值范围是 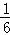 B.
B. 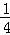 C.
C.  D.
D. 
 =1.732,
=1.732, =1.414.
=1.414.