题目内容
九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.
(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米,请你求出E点离地面FB的高度.
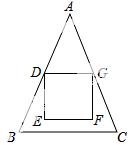
(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).
备用数据:tan60°=1.732,tan30°=0.577, =1.732,
=1.732, =1.414.
=1.414.

解:(1)∵BD=BC,
∴∠CDB=∠DCB,
∴∠α=2∠CDB=2×38°=76°.
(2)设EF的中点为M,过M作MN⊥BF,垂足为点N,
过点E作EH⊥BF,垂足为点H,
∵MN∥AH,MN=1.9,
∴EH=2MN=3.8(米),
∴E点离地面FB的高度是3.8米.
(3)延长AE,交PB于点C,
设AE=x,则AC=x+3.8,
∵∠APB=45°,
∴PC=AC=x+3.8,
∵PQ=4,
∴CQ=x+3.8﹣4=x﹣0.2,
∵tan∠AQC= =tan60°=
=tan60°= ,
,
∴ =
= ,
,
x= ≈5.7,
≈5.7,
∴AE≈5.7(米).
答;旗杆AE的高度是5.7米.



练习册系列答案
相关题目
 正确的结果是( )
正确的结果是( )  B.
B. C.
C. D.
D. 
 ﹣4sin45°﹣
﹣4sin45°﹣ +
+ .
.
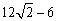 D.
D. 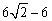
 示.
示.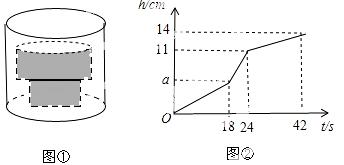
 (2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积.
(2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积. __________;
__________;