题目内容
已知⊙O1和⊙O2的半径分别为3和1,如果这两个圆相交,那么圆心距O1O2的取值范围在数轴上表示正确的是( )
A、 |
B、 |
C、 |
D、 |
考点:圆与圆的位置关系,在数轴上表示不等式的解集
专题:
分析:根据两圆的位置关系是相交,则这两个圆的圆心距d大于两半径之差小于两半径之和,从而解决问题.
解答:解:∵3-1=2,3+1=4,
∴2<p<4,
∴数轴上表示为A.
故选A.
∴2<p<4,
∴数轴上表示为A.
故选A.
点评:本题考查了由两圆半径和圆心距之间数量关系判断两圆位置关系的方法,设两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在0,-3,1,2这四个数中,最小的数是( )
| A、0 | B、-3 | C、1 | D、2 |
不等式组
的解集为( )
|
| A、x<2 | B、x≤1 |
| C、1<x<2 | D、1<x≤2 |
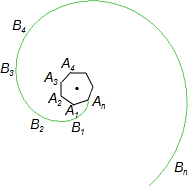 如图,正多边形A1、A2、A3、A4…An,曲线B1B2B3B4…Bn叫做“正多边形的渐开线”,其中AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环.循环一周就叫一周曲线长,当A1A2=1时,一周曲线长为
如图,正多边形A1、A2、A3、A4…An,曲线B1B2B3B4…Bn叫做“正多边形的渐开线”,其中AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环.循环一周就叫一周曲线长,当A1A2=1时,一周曲线长为 某一蓄水池的排水速度v(m3/h)与排水时间t(h)之间的图象满足函数关系:t=
某一蓄水池的排水速度v(m3/h)与排水时间t(h)之间的图象满足函数关系:t= 小南玩掷飞镖游戏,在他设计的一个由边长为1的小正方形组成的靶子中,有如图所示的A、B两点,投掷一次飞镖,则命中点与点A、B组成的三角形的面积大于
小南玩掷飞镖游戏,在他设计的一个由边长为1的小正方形组成的靶子中,有如图所示的A、B两点,投掷一次飞镖,则命中点与点A、B组成的三角形的面积大于
