题目内容
18.“日啖荔枝三百颗,不辞长作岭南人”,广东的夏季盛产荔枝,桂味、糯米糍是荔枝的品种之一.佳佳同学先用52元购买2千克桂味和1千克糯米糍;几天后,他用76元购买1千克桂味和3千克糯米糍.(前后两次两种荔枝的售价不变)(1)求桂味、糯米糍的售价分别是每千克多少元?
(2)若佳佳同学用y元买了这两种荔枝共中10千克,设买了x千克桂味.
①写出y与x的函数关系式.
②若要求糯米糍的重量不少于桂味重量的3倍,请帮佳佳同学设计一个购买方案,使所需的费用最少,并求出最少费用.
分析 (1)设桂味的售价是每千克m元,糯米糍的售价是每千克n元,根据“用52元购买2千克桂味和1千克糯米糍,用76元购买1千克桂味和3千克糯米糍”,即可得出关于m、n的二元一次方程组,解之即可得出结论;
(2)①设买了x千克桂味,则买了(10-x)千克糯米糍,根据总价=单价×购买数量,即可得出y与x的函数关系式;
②由糯米糍的重量不少于桂味重量的3倍可得出关于x的一元一次不等式,解之即可得出x的取值范围,再利用一次函数的性质即可解决最值问题.
解答 解:(1)设桂味的售价是每千克m元,糯米糍的售价是每千克n元,
根据题意得:$\left\{\begin{array}{l}{2m+n=52}\\{m+3n=76}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=16}\\{n=20}\end{array}\right.$.
答:桂味的售价是每千克16元,糯米糍的售价是每千克20元.
(2)①设买了x千克桂味,则买了(10-x)千克糯米糍,
根据题意得:y=16x+20(10-x)=-4x+200(0<x<10).
②∵糯米糍的重量不少于桂味重量的3倍,
∴10-x≥3x,
∴x≤$\frac{5}{2}$.
∵y=-4x+200中,k=-4<0,
∴y值随x值的增大而减小,
∴当x=$\frac{5}{2}$时,y取最小值,最小值为190.
答:当购买桂味$\frac{5}{2}$千克、糯米糍$\frac{15}{2}$千克时,所需的费用最少,最少费用为190元.
点评 本题考查了一次函数的应用、二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)①根据总价=单价×购买数量,列出y与x的函数关系式;②根据一次函数的性质解决最值问题.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | x2+7x+10=(x+2)(x+5) | B. | x2-2x-8=(x-4)(x+2) | C. | y2-7y+12=(y-3)(y-4) | D. | y2+7y-18=(y-6)(y+3) |
 如图,D为AB的中点,E为BC的中点,AD=2cm,EC=1.5cm,则DC=( )cm.
如图,D为AB的中点,E为BC的中点,AD=2cm,EC=1.5cm,则DC=( )cm.| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
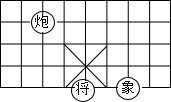 如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮“位于点(-1,1).
如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮“位于点(-1,1).