Question

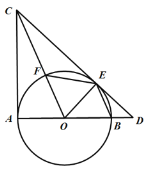
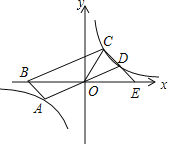
【题目】如图，在平面直角坐标系中，平行四边形ABCD的边AD经过O点，A、C、D三点都在反比例函数y＝的图象上，B点在x轴的负半轴上，延长CD交x轴于点E，连接CO．若S平行四边形ABCD＝6，则k的值为_____．

Answer 1

【答案】2

【解析】

作AH⊥OB于H，DG⊥y轴于G，CF⊥DG于F．首先证明△CFD≌△AHB，推出AH＝CF，DF＝BH，设A(m，)，则D(﹣m，﹣)，想办法构建方程即可解决问题．

作AH⊥OB于H，DG⊥y轴于G，CF⊥DG于F．

∵四边形ABCD是平行四边形，

∴AB＝CD，AB∥CD，

∵AH∥y轴∥CF，

∴∠BAH＝∠DCF，

∵∠DFC＝∠AHB，

∴△CFD≌△AHB(AAS)，

∴AH＝CF，DF＝BH，

设A(m，)，则D(﹣m，﹣)，

∵SABCD＝6，OA＝OD，

∴S△AOB＝，

∴OB＝，

∴OB＝ ，

∴CF＝AH＝，

∴C(﹣，﹣ )，

∵DF＝BH，

∴﹣﹣(﹣m)＝﹣m，

∴k＝2．

故答案为2．