题目内容
已知线段AB=10cm,直线AB上有一点C,且BC=4cm,M是线段BC的中点,则AM的长是 cm.
考点:两点间的距离
专题:
分析:应考虑到A、B、C三点之间的位置关系的多种可能,即点C在点B的右侧或点C在点B的左侧两种情况进行分类讨论.
解答: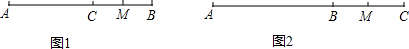 解:①如图1所示,当点C在点A与B之间时,
解:①如图1所示,当点C在点A与B之间时,
∵线段AB=10cm,BC=4cm,
∴AC=10-4=6cm.
∵M是线段BC的中点,
∴CM=
BC=2cm,
∴AM=AC+CM=6+2=8cm;
②当点C在点B的右侧时,
∵BC=4cm,M是线段BC的中点,
∴BM=
BC=2cm,
∴AM=AB+BM=10+2=12cm.
综上所述,线段AM的长为8cm或12cm.
故答案为:8或12.
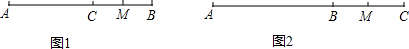 解:①如图1所示,当点C在点A与B之间时,
解:①如图1所示,当点C在点A与B之间时,∵线段AB=10cm,BC=4cm,
∴AC=10-4=6cm.
∵M是线段BC的中点,
∴CM=
| 1 |
| 2 |
∴AM=AC+CM=6+2=8cm;
②当点C在点B的右侧时,
∵BC=4cm,M是线段BC的中点,
∴BM=
| 1 |
| 2 |
∴AM=AB+BM=10+2=12cm.
综上所述,线段AM的长为8cm或12cm.
故答案为:8或12.
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
相关题目
 二次函数y=ax2+bx+c(a≠O)在平两直角坐标系内的图象如图所示,则图象与x轴
二次函数y=ax2+bx+c(a≠O)在平两直角坐标系内的图象如图所示,则图象与x轴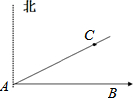 如图,测得A点到灯塔C点的距离为10海里,灯塔C点在A点东偏北30°方向上,一轮船由A点出发向正东方向航行,当此轮船行至距A点
如图,测得A点到灯塔C点的距离为10海里,灯塔C点在A点东偏北30°方向上,一轮船由A点出发向正东方向航行,当此轮船行至距A点