题目内容
9.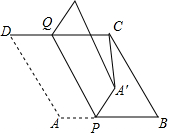 如图,在菱形ABCD中,AB=8,∠B=60°,P是AB上一点,BP=5,Q是CD边上一动点,将四边形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,则CQ的长为( )
如图,在菱形ABCD中,AB=8,∠B=60°,P是AB上一点,BP=5,Q是CD边上一动点,将四边形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,则CQ的长为( )| A. | 5 | B. | 6 | C. | 6.5 | D. | 7 |
分析 由A′P=3可知点A′在以P为圆心以PA′为半径的弧上,故此当C,P,A′在一条直线上时,CA′有最小值,过点C作CH⊥AB,垂足为H,先求得BH、HC的长,则可得到PH的长,然后再求得PC的长,最后依据折叠的性质和平行线的性质可证明△CQP为等腰三角形,则可得到QC的长.
解答 解:如图所示:过点C作CH⊥AB,垂足为H.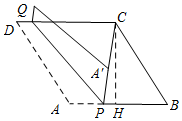
在Rt△BCH中,∠B=60°,BC=8,则BH=$\frac{1}{2}$BC=4,CH=sin60°•BC=$\frac{\sqrt{3}}{2}$×8=4$\sqrt{3}$.
∴PH=1.
在Rt△CPH中,依据勾股定理可知:PC=$\sqrt{(4\sqrt{3})^{2}+{1}^{2}}$=7.
由翻折的性质可知:∠APQ=∠A′PQ.
∵DC∥AB,
∴∠CQP=∠APQ.
∴∠CQP=∠CPQ.
∴QC=CP=7.
故选:D.
点评 本题主要考查的是菱形的性质、勾股定理的应用,翻折的性质、等腰三角形的判定,判断出CA′取得最小值的条件是解题的关键.

练习册系列答案
相关题目
14.如果一个多边形的内角和是外角和的2倍,则从这个多边形的一个顶点可以引( )条对角线.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.下列命题是真命题的是( )
| A. | 三角形的三条高线相交于三角形内一点 | |
| B. | 三角形的两边之和不大于第三边 | |
| C. | 有公共顶点且相等的两个角是对顶角 | |
| D. | 同角的补角相等 |
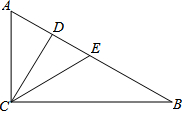 已知:直角三角形ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,AC=CE=10cm,则BD=15cm.
已知:直角三角形ABC中,∠ACB=90°,CD、CE分别是斜边上的高和中线,AC=CE=10cm,则BD=15cm. 已知如图,∠BOC与∠AOB互为补角,OD平分∠AOB,若∠COD=21°,求∠BOC的大小.
已知如图,∠BOC与∠AOB互为补角,OD平分∠AOB,若∠COD=21°,求∠BOC的大小.