题目内容
某公司生产的某种时令商品每件成本为20元,经过在本地市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
| 时间t(天) | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量m(件) | 94 | 90 | 84 | 76 | 24 | … |
 (1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为
(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为 (21≤t≤40且t为整数).下面我们就来研究销售这种商品的有关问题:
(21≤t≤40且t为整数).下面我们就来研究销售这种商品的有关问题:(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)请预测本地市场在未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在第30天,该公司在外地市场的销量比本地市场的销量增加a%还多30件,由于运输等原因,该商品每件成本比本地增加0.2a%少5元,在销售价格相同的情况下当日两地利润持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:
 ,
, ,
, ,
, ,
, )
)
解:(1)∵根据表格知道日销售量与时间t是均匀减少的,
∴确定m与t是一次函数关系,设函数关系式为:m=kt+b,
∵当t=1,m=94;当t=3,m=90,
∴ ,
,
解之得: ,
,
∴m=-2t+96;
(2)前20天:
∵每天的价格y(元)与时间t天的函数关系式为y= t+25,
t+25,
而商品每件成本为20元,
∴每件获取的利润为( t+25-20)=(
t+25-20)=( t+5)元,
t+5)元,
又日销售量y(件)与时间t(天)的函数关系式为:y=-2t+96,
故:前20天每天获取的利润:
P=( t+5)(-2t+96)
t+5)(-2t+96)
=- t2+14t+480
t2+14t+480
∴P=- (t-14)2+578 (1≤t≤20)
(t-14)2+578 (1≤t≤20)
根据二次函数的相关性质可知:t=14时,日获利润最大,且为578元;
后20天:
每天的价格y(元)与时间t天的函数关系式为y=- t+40,
t+40,
而商品每件成本为20元,
故每件获取的利润为(- t+40-20)=(-
t+40-20)=(- t+20)元,
t+20)元,
又日销售量y(件)与时间t(天)的函数关系式为:y=-2t+96,
故:后20天每天获取的利润
P=(- t+20)(-2t+96)
t+20)(-2t+96)
=t2-88t+1920,
∴P=(t-44)2-16 (21≤t≤40),
根据二次函数的相关性质可知:
当t=21时,日获利润最大,且为513元
综合以上:t=14时,日获利润最大,且为578元;
(3)在第30天,本地的销售量为m=-2×30+96=36,销售价格为:y=- ×30+40=25,
×30+40=25,
依题意得公司在外地市场的销量为:36×(1+a%)+30,
依题意得:36×(25-20)=[36×(1+a%)+30][25-20(1+0.2a%)+5],
整理得:3(a%) 2-2a%-10=0,
解得:a%= ,则a%1=
,则a%1=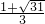 =
= ≈219%,a%2=
≈219%,a%2= <0(不合题意舍去),
<0(不合题意舍去),
故a≈219.
分析:(1)通过观察表格中的数据日销售量与时间t是均匀减少的,所以确定m与t是一次函数关系,利用待定系数法即可求出函数关系式;
(2)分前20天和后20天分别讨论:根据日销售量、每天的价格及时间t可以列出销售利润W关于t的二次函数,然后利用二次函数的性质即可求出哪一天的日销售利润最大,最大日销售利润是多少;
(3)由于在第30天,利用(1)中结论和已知条件可以求出本地的利润,也可以根据该公司在外地市场的销量比本地市场的销量增加a%还多30件,由于运输等原因,该商品每件成本比本地增加0.2a%少5元,可以用a列出外地销售利润,然后根据在销售价格相同的情况下当日两地利润持平可以列出关于a的方程,解方程即可求解.
点评:此题分别考查了二次函数的应用,一元二次方程的应用等知识,解题的关键 首先读懂题目,正确把握题目的数量关系,根据数量关系分别列出函数关系式和一元二次方程解决问题.
∴确定m与t是一次函数关系,设函数关系式为:m=kt+b,
∵当t=1,m=94;当t=3,m=90,
∴
 ,
,解之得:
 ,
,∴m=-2t+96;
(2)前20天:
∵每天的价格y(元)与时间t天的函数关系式为y=
 t+25,
t+25,而商品每件成本为20元,
∴每件获取的利润为(
 t+25-20)=(
t+25-20)=( t+5)元,
t+5)元,又日销售量y(件)与时间t(天)的函数关系式为:y=-2t+96,
故:前20天每天获取的利润:
P=(
 t+5)(-2t+96)
t+5)(-2t+96)=-
 t2+14t+480
t2+14t+480∴P=-
 (t-14)2+578 (1≤t≤20)
(t-14)2+578 (1≤t≤20)根据二次函数的相关性质可知:t=14时,日获利润最大,且为578元;
后20天:
每天的价格y(元)与时间t天的函数关系式为y=-
 t+40,
t+40,而商品每件成本为20元,
故每件获取的利润为(-
 t+40-20)=(-
t+40-20)=(- t+20)元,
t+20)元,又日销售量y(件)与时间t(天)的函数关系式为:y=-2t+96,
故:后20天每天获取的利润
P=(-
 t+20)(-2t+96)
t+20)(-2t+96)=t2-88t+1920,
∴P=(t-44)2-16 (21≤t≤40),
根据二次函数的相关性质可知:
当t=21时,日获利润最大,且为513元
综合以上:t=14时,日获利润最大,且为578元;
(3)在第30天,本地的销售量为m=-2×30+96=36,销售价格为:y=-
 ×30+40=25,
×30+40=25,依题意得公司在外地市场的销量为:36×(1+a%)+30,
依题意得:36×(25-20)=[36×(1+a%)+30][25-20(1+0.2a%)+5],
整理得:3(a%) 2-2a%-10=0,
解得:a%=
 ,则a%1=
,则a%1=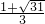 =
= ≈219%,a%2=
≈219%,a%2= <0(不合题意舍去),
<0(不合题意舍去),故a≈219.
分析:(1)通过观察表格中的数据日销售量与时间t是均匀减少的,所以确定m与t是一次函数关系,利用待定系数法即可求出函数关系式;
(2)分前20天和后20天分别讨论:根据日销售量、每天的价格及时间t可以列出销售利润W关于t的二次函数,然后利用二次函数的性质即可求出哪一天的日销售利润最大,最大日销售利润是多少;
(3)由于在第30天,利用(1)中结论和已知条件可以求出本地的利润,也可以根据该公司在外地市场的销量比本地市场的销量增加a%还多30件,由于运输等原因,该商品每件成本比本地增加0.2a%少5元,可以用a列出外地销售利润,然后根据在销售价格相同的情况下当日两地利润持平可以列出关于a的方程,解方程即可求解.
点评:此题分别考查了二次函数的应用,一元二次方程的应用等知识,解题的关键 首先读懂题目,正确把握题目的数量关系,根据数量关系分别列出函数关系式和一元二次方程解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某公司生产的某种时令商品每件成本为20元,经过在本地市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1=
t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=-
t+40(21≤t≤40且t为整数).下面我们就来研究销售这种商品的有关问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)请预测本地市场在未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在第30天,该公司在外地市场的销量比本地市场的销量增加a%还多30件,由于运输等原因,该商品每件成本比本地增加0.2a%少5元,在销售价格相同的情况下当日两地利润持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:
≈5.39,
≈5.48,
≈5.57,
≈5.66,
≈5.74)
| 时间t(天) | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量m(件) | 94 | 90 | 84 | 76 | 24 | … |
| 1 |
| 4 |
| 1 |
| 2 |
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)请预测本地市场在未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在第30天,该公司在外地市场的销量比本地市场的销量增加a%还多30件,由于运输等原因,该商品每件成本比本地增加0.2a%少5元,在销售价格相同的情况下当日两地利润持平,请你参考以下数据,通过计算估算出a的整数值.
(参考数据:
| 29 |
| 30 |
| 31 |
| 32 |
| 33 |
某公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
| 时间t(天) | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量m(件) | 94 | 90 | 84 | 76 | 24 | … |
 (
( 且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式
且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式 为
 (
( 且t为整数). 下面我们就来研究销售这种商品的有关问题:(1)分析上表中的数据,确定一个满足这些数据的m(件)与t(天)之间的关系式;
且t为整数). 下面我们就来研究销售这种商品的有关问题:(1)分析上表中的数据,确定一个满足这些数据的m(件)与t(天)之间的关系式;(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程. 公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
某公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
|
时间t(天) |
1 |
3 |
6 |
10 |
36 |
… |
|
日销售量m(件) |
94 |
90 |
84 |
76 |
24 |
… |
未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为 (
( 且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式
且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式
为 (
( 且t为整数). 下面我们就来研究销售这种商品的有关问题:(1)分析上表中的数据,确定一个满足这些数据的m(件)与t(天)之间的关系式;
且t为整数). 下面我们就来研究销售这种商品的有关问题:(1)分析上表中的数据,确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程. 公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
 程.公司通过销售记录发现,前20天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
程.公司通过销售记录发现,前20天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.