题目内容
【题目】如图，四边形
中，
，
，
，将
绕点
逆时针旋转
得到
，连接
，过点作
于点
，交
于点
．
（1）如图，
．
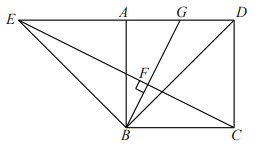
①求证：四边形是正方形；
②求证：是中点；
（2）如图，若
，请判断是否仍然是的中点？若是，请证明；若不是，请说明理由．
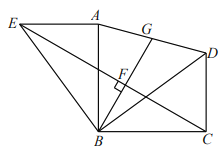
【答案】（1）①详见解析；②详见解析；（2）点 
仍然是
的中点，证明详见解析.
【解析】
（1）①根据题意得出四边形 
是平行四边形，再由
，
，得出矩形是正方形．②由①得出
，从而得到
，再求出
，即可解答
（2）延长
，
交于点
，延长
交 
于点
,先求出矩形
是正方形
在证明
，从而得出
，即可解答
（1）证明：①
，
，
四边形 是平行四边形，
，
平行四边形是矩形．
，
矩形是正方形．
②由①得
，
．
由旋转得，
，
，
，
．
，
，
．
，
，
．
，
，
，
，
，
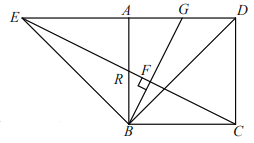
是的中点．
（2）点 仍然是的中点．
证明如下：延长，交于点，延长交 于点．
，，
，
，
．
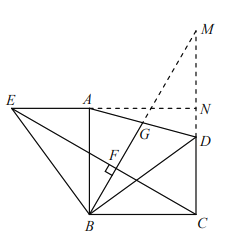
由旋转得，
，
，
，
四边形是矩形．
，
矩形是正方形，
，
，
．
，
，
，
，
，
，
即
，
，
，
，
是
中点．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
