题目内容
6.已知2a=3,2b=7,2c=42,求证:a+b+1=c.分析 首先根据同底数幂的乘法法则,可得2a+b=2a•2b=3×7=21,所以2a+b+1=2×21=42;然后根据2c=42,推得2a+b+1=2c,判断出a+b+1=c即可.
解答 证明:∵2a=3,2b=7,
∴2a+b=2a•2b=3×7=21,
∴2a+b+1=2×21=42;
又∵2c=42,
∴2a+b+1=2c,
∴a+b+1=c.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).
(2)此题还考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.

练习册系列答案
相关题目
16.已知|a|=1,|b|=3,则|a+b|的值为( )
| A. | 2 | B. | 4 | C. | 2或4 | D. | ±2或±4. |
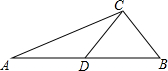 如图,在△ABC中,AB边上的中线CD=3,AB=6,BC+AC=8,
如图,在△ABC中,AB边上的中线CD=3,AB=6,BC+AC=8,