题目内容
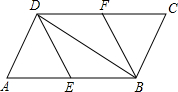 如图,在四边形ABCD中,AD∥BC,BD⊥AD,点E,F分别是边AB,CD的中点,且DE=BF.求证:∠A=∠C.
如图,在四边形ABCD中,AD∥BC,BD⊥AD,点E,F分别是边AB,CD的中点,且DE=BF.求证:∠A=∠C.考点:全等三角形的判定与性质
专题:证明题
分析:首先根据平行线的性质可得∠DBC=∠BDA=90°,再根据直角三角形的性质可得DE=
AB,BF=
DC,然后可得AB=CD,再证明Rt△ADB≌Rt△CBD可得∠A=∠C.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵AD∥BC,BD⊥AD,
∴∠DBC=∠BDA=90°,
∵在Rt△ADB中,E是AB的中线,
∴DE=
AB,
同理:BF=
DC,
∵DE=BF,
∴AB=CD,
在Rt△ADB和Rt△CBD中,
,
∴Rt△ADB≌Rt△CBD(HL),
∴∠A=∠C.
∴∠DBC=∠BDA=90°,
∵在Rt△ADB中,E是AB的中线,
∴DE=
| 1 |
| 2 |
同理:BF=
| 1 |
| 2 |
∵DE=BF,
∴AB=CD,
在Rt△ADB和Rt△CBD中,
|
∴Rt△ADB≌Rt△CBD(HL),
∴∠A=∠C.
点评:此题主要考查了全等三角形的判定与性质,关键是找出证明Rt△ADB≌Rt△CBD的条件.

练习册系列答案
相关题目
 某高校图书馆整理图书,把图书馆内的书分成三类,A.表示科技类,B.表示哲学类,C.表示艺术类,所占的百分比如图所示,如果该校图书馆共有8500册,则艺术类图书馆共有
某高校图书馆整理图书,把图书馆内的书分成三类,A.表示科技类,B.表示哲学类,C.表示艺术类,所占的百分比如图所示,如果该校图书馆共有8500册,则艺术类图书馆共有 如图,边长为1的小正方形构成的网格中,⊙O的半径为1,则图中阴影部分两个小扇形的面积之和为
如图,边长为1的小正方形构成的网格中,⊙O的半径为1,则图中阴影部分两个小扇形的面积之和为