题目内容
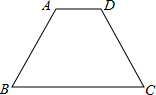如图，在梯形ABCD中，AD∥BC，∠B=∠C=60°，AD=15cm，BC=49cm．求AB的长．考点：梯形
专题：
分析：过点A作AE∥CD交BC于点E，则可得△ABE是等边三角形，求出BE的长度，即可得出AB的长度．
解答：解：过点A作AE∥CD交BC于点E，则四边形ADCE是平行四边形，
∵AD∥BC，∠B=∠C=60°，
∴四边形ABCD是等腰梯形，
∴AE=CD=AB，
又∵∠B=60°，
∴△ABE是等边三角形，
∴AB=BE=BC-CE=BC-AD=34cm．
∵AD∥BC，∠B=∠C=60°，
∴四边形ABCD是等腰梯形，
∴AE=CD=AB，
又∵∠B=60°，
∴△ABE是等边三角形，
∴AB=BE=BC-CE=BC-AD=34cm．
点评：本题考查了等腰梯形的判定和性质，解答本题的关键是作出辅助线，过顶点作一腰的平行线是解答梯形有关问题时经常用到的辅助线，需要引起同学们的注意．
练习册系列答案
相关题目
下面关于有理数的说法正确的是（ ）
| A、有理数可分为正有理数和负有理数两大类 |
| B、整数集合可分为正整数集合和负整数集合 |
| C、整数和分数统称为有理数 |
| D、正数和负数统称为有理数 |
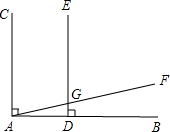如图，已知AC⊥AB，ED⊥AB，∠CAF=78°，求∠DGF的度数．
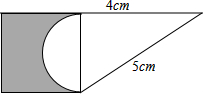如图所示是由一个正方形、一个直角三角形和一个半圆组成的图形，试求阴影部分的面积．
如图，图中的箭头A，点A′是A的轴对称点，请用铅笔画出箭头A′．