题目内容
关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根 .
.
(1)(4分)求实数k的取值范围.
(2)(4分)若方程两实根 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值.
(1)∵原方程有两个不相等的实数根
∴ Δ= 2-
2- 2+1)=4k2+4k+1-4k2-4=4k-3﹥0
2+1)=4k2+4k+1-4k2-4=4k-3﹥0
解得:k﹥
(2) ∵k﹥ ∴ x1+ x2 =-(2k+1)<0 又∵ x1·x2 = k2+1﹥0
∴ x1+ x2 =-(2k+1)<0 又∵ x1·x2 = k2+1﹥0
∴x1<0,x2 <0 ∴|x1|+|x2|=-x1-x2 =-(x1+x2)=2k+1
∵|x1|+|x2|= x1·x2 ∴2k+1=k2+1 ∴ k1=0, k2=2 ………7′
 又 ∵k﹥
又 ∵k﹥ ∴k=2
∴k=2

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 的结果是
的结果是 B、
B、 C、
C、 D、
D、

 C.
C. D.
D.

 ,连接PB,则PB= .
,连接PB,则PB= . 一次函数
一次函数 (
( 为常数)与反比例函数
为常数)与反比例函数  的图象交于A、B两
的图象交于A、B两 点,当A、B两点关于原点对称时
点,当A、B两点关于原点对称时 90°.
90°.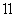 如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由; 如图2,在旋转过程中,当∠DOM
如图2,在旋转过程中,当∠DOM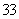 如图3,旋转后,
如图3,旋转后, 若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD
若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD
