题目内容
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于
于![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,求证:
,求证:
![]() ;
;
![]() ;
;
![]() 是等腰直角三角形.
是等腰直角三角形.
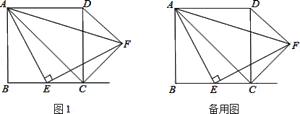
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)取AB中点M,连接ME,利用正方形的性质和等腰直角三角形的性质,证明△AME△ECF,即可得出结论;
(2)利用(1)图,△AEF是等腰直角三角形,继而得到∠2=∠4、∠ACF=∠B,即可证得结论;
(3)过F分别作FN⊥BC的延长线于N,证得△FNE△EBA,得出△FCN是等腰直角三角形,易证四边形FNCP为矩形(正方形),求得∠FDC=∠DCF,得出结论.
![]() 如图
如图![]() ,
,

取![]() 中点
中点![]() ,连接
,连接![]() ,
,
则![]() 正方形边长,
正方形边长,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() 是正方形外角的平分线,
是正方形外角的平分线,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ;
;
![]() 如图
如图![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,即
,即![]() ,
,
∵![]() 为正方形
为正方形![]() 的对角线,
的对角线,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 如图
如图![]() ,
,

设正方形![]() 边长为
边长为![]() ,则
,则![]() ,
,![]() ,
,
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
过![]() 作
作![]() 的延长线于
的延长线于![]() ,
,
则![]() ,
,
又由![]() 知,
知,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形(正方形),
为矩形(正方形),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形.
是等腰直角三角形.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目