题目内容
 有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正确水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行
有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正确水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行
- A.2.76米
- B.6.76米
- C.6米
- D.7米
B
分析:根据已知,假设解析式为y=ax2,把(10,-4)代入求出解析式.假设在水面宽度18米时,能顺利通过,即可把x=9代入解析式,求出此时水面距拱顶的高度,然后和正常水位相比较即可解答.
解答:设该抛物线的解析式为y=ax2,在正常水位下x=10,代入解析式可得-4=a×102?a=-
故此抛物线的解析式为y=- x2.
x2.
因为桥下水面宽度不得小于18米
所以令x=9时
可得y= =-3.24米
=-3.24米
此时水深6+4-3.24=6.76米
即桥下水深6.76米时正好通过,所以超过6.76米时则不能通过.
故选B.
点评:本题考查点的坐标的求法及二次函数的实际应用,借助二次函数解决实际问题.难度中上,首先要知道水面宽度与水位上升高度的关系才能求解.
分析:根据已知,假设解析式为y=ax2,把(10,-4)代入求出解析式.假设在水面宽度18米时,能顺利通过,即可把x=9代入解析式,求出此时水面距拱顶的高度,然后和正常水位相比较即可解答.
解答:设该抛物线的解析式为y=ax2,在正常水位下x=10,代入解析式可得-4=a×102?a=-

故此抛物线的解析式为y=-
 x2.
x2.因为桥下水面宽度不得小于18米
所以令x=9时
可得y=
 =-3.24米
=-3.24米此时水深6+4-3.24=6.76米
即桥下水深6.76米时正好通过,所以超过6.76米时则不能通过.
故选B.
点评:本题考查点的坐标的求法及二次函数的实际应用,借助二次函数解决实际问题.难度中上,首先要知道水面宽度与水位上升高度的关系才能求解.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目

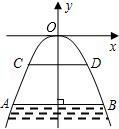 如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.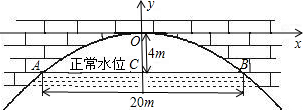
 有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米;
有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米;