题目内容
孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线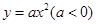 的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点
的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点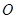 ,两直角边与该抛物线交于
,两直角边与该抛物线交于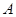 、
、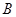 两点,请解答以下问题:
两点,请解答以下问题:
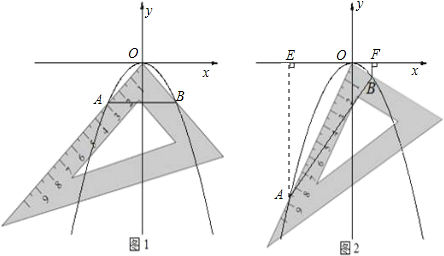
(1)若测得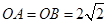 (如图1),求
(如图1),求 的值;
的值;
(2)对同一条抛物线,孔明将三角板绕点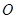 旋转到如图2所示位置时,过
旋转到如图2所示位置时,过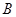 作
作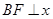 轴于点
轴于点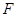 ,测得
,测得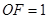 ,写出此时点
,写出此时点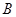 的坐标,并求点
的坐标,并求点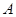 的横坐标;
的横坐标;
(3)对该抛物线,孔明将三角板绕点 旋转任意角度时惊奇地发现,交点
旋转任意角度时惊奇地发现,交点 、
、 的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
的连线段总经过一个固定的点,试说明理由并求出该点的坐标.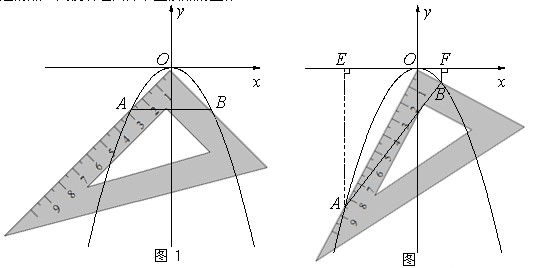
(1)设线段 与
与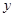 轴的交点为
轴的交点为 ,由抛物线的对称性可得
,由抛物线的对称性可得 为
为 中点,
中点,
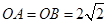 ,
, ,
,
 ,
,
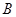 (
( ,
, )
)
将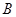 (
( ,
, )代入抛物线
)代入抛物线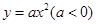 得,
得, .
.
(2)解法一:过点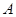 作
作 轴于点
轴于点 ,
,
 点
点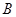 的横坐标为
的横坐标为 ,
,
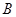 (1,
(1, ),
), 
 . 又
. 又
 ,易知
,易知 ,又
,又 ,
, △
△ ∽△
∽△ ,
,



设点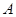 (
( ,
, )(
)( ),则
),则 ,
, ,
,


 ,即点
,即点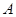 的横坐标为
的横坐标为 .
.
解法二:过点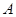 作
作 轴于点
轴于点 ,
, 点
点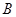 的横坐标为
的横坐标为 ,
,
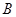 (1,
(1, ),
),
设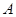 (-
(- ,
, )(
)( ),则
),则 ,
, ,
, ,
, 


解析

练习册系列答案
相关题目

 (如图1),求a的值;
(如图1),求a的值;
 (如图1),求a的值;
(如图1),求a的值;
 (如图1),求a的值;
(如图1),求a的值;