ЬтФПФкШн
ПзУїЪЧвЛИіЯВЛЖЬНОПзъбаЕФЭЌбЇЃЌЫћдкКЭЭЌбЇУЧвЛЦ№баОПФГЬѕХзЮяЯпy=ax2ЃЈaЃМ0ЃЉЕФаджЪЪБЃЌНЋвЛАбжБНЧШ§НЧАхЕФжБНЧЖЅЕужУгкЦНУцжБНЧзјБъЯЕЕФдЕуOЃЌСНжБНЧБпгыИУХзЮяЯпНЛгкAЁЂBСНЕуЃЌЧыНтД№вдЯТЮЪЬтЃКЃЈ1ЃЉШєВтЕУOA=OB=2
| 2 |
ЃЈ2ЃЉЖдЭЌвЛЬѕХзЮяЯпЃЌПзУїНЋШ§НЧАхШЦЕуOа§зЊЕНШчЭМ2ЫљЪОЮЛжУЪБЃЌЙ§BзїBFЁЭxжсгкЕуFЃЌВтЕУOF=1ЃЌаДГіДЫЪБЕуBЕФзјБъЃЌВЂЧѓЕуAЕФКсзјБъ
ЃЈ3ЃЉЖдИУХзЮяЯпЃЌПзУїНЋШ§НЧАхШЦЕуOа§зЊШЮвтНЧЖШЪБОЊЦцЕиЗЂЯжЃЌНЛЕуAЁЂBЕФСЌЯпЖЮзмОЙ§вЛИіЙЬЖЈЕФЕуЃЌЪдЫЕУїРэгЩВЂЧѓГіИУЕуЕФзјБъЃЎ
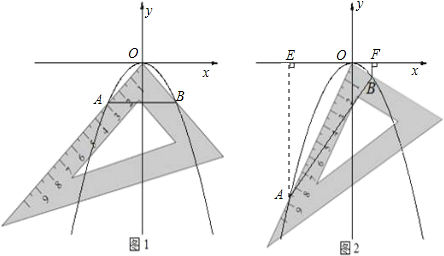
ЗжЮіЃКЃЈ1ЃЉЯШЧѓГіBЕузјБъЃЌДњШыХзЮяЯпy=ax2ЃЈaЃМ0ЃЉЕУaЕФжЕЃЛ
ЃЈ2ЃЉЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌПЩжЄЁїAEOЁзЁїOFBЃЌЕУГіAE=2OEЃЌПЩЕУЗНГЬЕуAЕФКсзјБъЃЎ
ЃЈ3ЃЉЩшAЃЈ-mЃЌ-
m2ЃЉЃЈmЃО0ЃЉЃЌBЃЈnЃЌ-
n2ЃЉЃЈnЃО0ЃЉЃЌвзжЊЁїAEOЁзЁїOFBЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪПЩжЊНЛЕуAЁЂBЕФСЌЯпЖЮзмОЙ§вЛИіЙЬЖЈЕФЕуЃЈ0ЃЌ-2ЃЉЃЎ
ЃЈ2ЃЉЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌПЩжЄЁїAEOЁзЁїOFBЃЌЕУГіAE=2OEЃЌПЩЕУЗНГЬЕуAЕФКсзјБъЃЎ
ЃЈ3ЃЉЩшAЃЈ-mЃЌ-
| 1 |
| 2 |
| 1 |
| 2 |
НтД№ЃК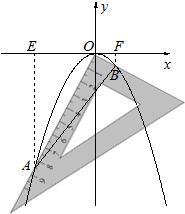 НтЃКЃЈ1ЃЉЩшЯпЖЮABгыyжсЕФНЛЕуЮЊCЃЌгЩХзЮяЯпЕФЖдГЦадПЩЕУCЮЊABжаЕуЃЌ
НтЃКЃЈ1ЃЉЩшЯпЖЮABгыyжсЕФНЛЕуЮЊCЃЌгЩХзЮяЯпЕФЖдГЦадПЩЕУCЮЊABжаЕуЃЌ
ЁпOA=OB=2
ЃЌЁЯAOB=90ЁуЃЌ
ЁрAC=OC=BC=2ЃЌ
ЁрBЃЈ2ЃЌ-2ЃЉЃЌ
НЋBЃЈ2ЃЌ-2ЃЉДњШыХзЮяЯпy=ax2ЃЈaЃМ0ЃЉЕУЃЌa=-
ЃЎ
ЃЈ2ЃЉНтЗЈвЛЃКЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌ
ЁпЕуBЕФКсзјБъЮЊ1ЃЌ
ЁрBЃЈ1ЃЌ-
ЃЉЃЌ
ЁрBF=
ЃЎ
гжЁпЁЯAOB=90ЁуЃЌвзжЊЁЯAOE=ЁЯOBFЃЌ
гжЁпЁЯAEO=ЁЯOFB=90ЁуЃЌ
ЁрЁїAEOЁзЁїOFBЃЌ
Ёр
=
=
=2ЃЌ
ЁрAE=2OEЃЌ
ЩшЕуAЃЈ-mЃЌ-
m2ЃЉЃЈmЃО0ЃЉЃЌдђOE=mЃЌ
AE=
m2ЃЌ
Ёр
m2=2mЃЌ
Ёрm=4ЃЌМДЕуAЕФКсзјБъЮЊ-4ЃЎ
НтЗЈЖўЃКЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌ
ЁпЕуBЕФКсзјБъЮЊ1ЃЌ
ЁрBЃЈ1ЃЌ-
ЃЉЃЌ
ЁрtanЁЯOBF=
=
=2ЃЌ
ЁпЁЯAOB=90ЁуЃЌвзжЊЁЯAOE=ЁЯOBFЃЌ
Ёр
=tanЁЯAOE=tanЁЯOBF=2ЃЌ
ЁрAE=2OEЃЌ
ЩшЕуAЃЈ-mЃЌ-
m2ЃЉЃЈmЃО0ЃЉЃЌ
дђOE=mЃЌAE=
m2ЃЌ
Ёр
m2=2mЃЌ
Ёрm=4ЃЌМДЕуAЕФКсзјБъЮЊ-4ЃЎ
НтЗЈШ§ЃКЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌ
ЁпЕуBЕФКсзјБъЮЊ1ЃЌ
ЁрBЃЈ1ЃЌ-
ЃЉЃЌ
ЩшAЃЈ-mЃЌ-
m2ЃЉЃЈmЃО0ЃЉЃЌ
дђOB2=12+(
)2=
ЃЌOA2=m2+
m4ЃЌAB2=(1+m)2+(-
+
m2)2ЃЌ
ЁпЁЯAOB=90Ёу
ЁрAB2=OA2+OB2ЃЌ
ЁрЃЈ1+mЃЉ2+ЃЈ-
+
m2ЃЉ2=
+m2+
m4ЃЌ
НтЕУЃКm=4ЃЌМДЕуAЕФКсзјБъЮЊ-4ЃЎ
ЃЈ3ЃЉНтЗЈвЛЃКЩшAЃЈ-mЃЌ-
m2ЃЉЃЈmЃО0ЃЉЃЌBЃЈnЃЌ-
n2ЃЉЃЈnЃО0ЃЉЃЌ
ЩшжБЯпABЕФНтЮіЪНЮЊЃКy=kx+bЃЌдђ
ЃЌ
ЃЈ1ЃЉЁСn+ЃЈ2ЃЉЁСmЕУЃЌ(m+n)b=-
(m2n+mn2)=-
mn(m+n)ЃЌ
Ёрb=-
mnЃЈ8ЗжЃЉ
гжвзжЊЁїAEOЁзЁїOFBЃЌ
Ёр
=
ЃЌ
Ёр
=
ЃЌ
Ёрmn=4ЃЌ
Ёрb=-
ЁС4=-2ЃЎ
гЩДЫПЩжЊВЛТлkЮЊКЮжЕЃЌжБЯпABКуЙ§ЕуЃЈ0ЃЌ-2ЃЉЃЎ
ЃЈЫЕУїЃКаДГіЖЈЕуCЕФзјБъОЭИј2ЗжЃЉ
НтЗЈЖўЃКЁпЕуAЪЧХзЮяЯпy=-
x2ЩЯЕФЕуЃЌ
ЁрЩшAЃЈ-mЃЌ-
m2ЃЉЃЈmЃО0ЃЉЃЌBЃЈnЃЌ-
n2ЃЉЃЈnЃО0ЃЉЃЌ
жБЯпABгыyжсЕФНЛЕуЮЊCЃЌИљОнSЁїAOB=SЬнаЮABFE-SЁїAOE-SЁїB0F=SЁїAOC+SЁїBOCЃЌ
ПЩЕУ
•(
n2+
m2)(m+n)-
•m•
m2-
•n•
n2=
•OC•m+
•OC•nЃЌ
ЛЏМђЃЌЕУOC=
mnЃЎ
гжвзжЊЁїAEOЁзЁїOFBЃЌ
Ёр
=
ЃЌ
Ёр
=
ЃЌ
Ёрmn=4ЃЌ
ЁрOC=2ЮЊЙЬЖЈжЕЃЎЙЪжБЯпABКуЙ§ЦфгыyжсЕФНЛЕуCЃЈ0ЃЌ-2ЃЉЃЌ
ЫЕУїЃКmnЕФжЕвВПЩвдЭЈЙ§вдЯТЗНЗЈЧѓЕУЃЎ
гЩЧАПЩжЊЃЌOA2=m2+
m4ЃЌOB2=n2+
n4ЃЌAB2=(m+n)2+(-
m2+
n2)2ЃЌ
гЩOA2+OB2=AB2ЃЌЕУЃК(m2+
m4)+(n2+
n4)=(m+n)2+(-
m2+
n2)2ЃЌ
ЛЏМђЃЌЕУmn=4ЃЎ
БОД№АИНіЙЉВЮПМЃЌШєгаЦфЫћНтЗЈЃЌЧыВЮееБОЦРЗжБъзМЦРЗжЃЎ
 НтЃКЃЈ1ЃЉЩшЯпЖЮABгыyжсЕФНЛЕуЮЊCЃЌгЩХзЮяЯпЕФЖдГЦадПЩЕУCЮЊABжаЕуЃЌ
НтЃКЃЈ1ЃЉЩшЯпЖЮABгыyжсЕФНЛЕуЮЊCЃЌгЩХзЮяЯпЕФЖдГЦадПЩЕУCЮЊABжаЕуЃЌЁпOA=OB=2
| 2 |
ЁрAC=OC=BC=2ЃЌ
ЁрBЃЈ2ЃЌ-2ЃЉЃЌ
НЋBЃЈ2ЃЌ-2ЃЉДњШыХзЮяЯпy=ax2ЃЈaЃМ0ЃЉЕУЃЌa=-
| 1 |
| 2 |
ЃЈ2ЃЉНтЗЈвЛЃКЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌ
ЁпЕуBЕФКсзјБъЮЊ1ЃЌ
ЁрBЃЈ1ЃЌ-
| 1 |
| 2 |
ЁрBF=
| 1 |
| 2 |
гжЁпЁЯAOB=90ЁуЃЌвзжЊЁЯAOE=ЁЯOBFЃЌ
гжЁпЁЯAEO=ЁЯOFB=90ЁуЃЌ
ЁрЁїAEOЁзЁїOFBЃЌ
Ёр
| AE |
| OE |
| OF |
| BF |
| 1 | ||
|
ЁрAE=2OEЃЌ
ЩшЕуAЃЈ-mЃЌ-
| 1 |
| 2 |
AE=
| 1 |
| 2 |
Ёр
| 1 |
| 2 |
Ёрm=4ЃЌМДЕуAЕФКсзјБъЮЊ-4ЃЎ
НтЗЈЖўЃКЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌ
ЁпЕуBЕФКсзјБъЮЊ1ЃЌ
ЁрBЃЈ1ЃЌ-
| 1 |
| 2 |
ЁрtanЁЯOBF=
| OF |
| BF |
| 1 | ||
|
ЁпЁЯAOB=90ЁуЃЌвзжЊЁЯAOE=ЁЯOBFЃЌ
Ёр
| AE |
| OE |
ЁрAE=2OEЃЌ
ЩшЕуAЃЈ-mЃЌ-
| 1 |
| 2 |
дђOE=mЃЌAE=
| 1 |
| 2 |
Ёр
| 1 |
| 2 |
Ёрm=4ЃЌМДЕуAЕФКсзјБъЮЊ-4ЃЎ
НтЗЈШ§ЃКЙ§ЕуAзїAEЁЭxжсгкЕуEЃЌ
ЁпЕуBЕФКсзјБъЮЊ1ЃЌ
ЁрBЃЈ1ЃЌ-
| 1 |
| 2 |
ЩшAЃЈ-mЃЌ-
| 1 |
| 2 |
дђOB2=12+(
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
ЁпЁЯAOB=90Ёу
ЁрAB2=OA2+OB2ЃЌ
ЁрЃЈ1+mЃЉ2+ЃЈ-
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 4 |
НтЕУЃКm=4ЃЌМДЕуAЕФКсзјБъЮЊ-4ЃЎ
ЃЈ3ЃЉНтЗЈвЛЃКЩшAЃЈ-mЃЌ-
| 1 |
| 2 |
| 1 |
| 2 |
ЩшжБЯпABЕФНтЮіЪНЮЊЃКy=kx+bЃЌдђ
|
ЃЈ1ЃЉЁСn+ЃЈ2ЃЉЁСmЕУЃЌ(m+n)b=-
| 1 |
| 2 |
| 1 |
| 2 |
Ёрb=-
| 1 |
| 2 |
гжвзжЊЁїAEOЁзЁїOFBЃЌ
Ёр
| AE |
| OF |
| OE |
| BF |
Ёр
| 0.5m2 |
| n |
| m |
| 0.5n2 |
Ёрmn=4ЃЌ
Ёрb=-
| 1 |
| 2 |
гЩДЫПЩжЊВЛТлkЮЊКЮжЕЃЌжБЯпABКуЙ§ЕуЃЈ0ЃЌ-2ЃЉЃЎ
ЃЈЫЕУїЃКаДГіЖЈЕуCЕФзјБъОЭИј2ЗжЃЉ
НтЗЈЖўЃКЁпЕуAЪЧХзЮяЯпy=-
| 1 |
| 2 |
ЁрЩшAЃЈ-mЃЌ-
| 1 |
| 2 |
| 1 |
| 2 |
жБЯпABгыyжсЕФНЛЕуЮЊCЃЌИљОнSЁїAOB=SЬнаЮABFE-SЁїAOE-SЁїB0F=SЁїAOC+SЁїBOCЃЌ
ПЩЕУ
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
ЛЏМђЃЌЕУOC=
| 1 |
| 2 |
гжвзжЊЁїAEOЁзЁїOFBЃЌ
Ёр
| AE |
| OF |
| OE |
| BF |
Ёр
| 0.5m2 |
| n |
| m |
| 0.5n2 |
Ёрmn=4ЃЌ
ЁрOC=2ЮЊЙЬЖЈжЕЃЎЙЪжБЯпABКуЙ§ЦфгыyжсЕФНЛЕуCЃЈ0ЃЌ-2ЃЉЃЌ
ЫЕУїЃКmnЕФжЕвВПЩвдЭЈЙ§вдЯТЗНЗЈЧѓЕУЃЎ
гЩЧАПЩжЊЃЌOA2=m2+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
гЩOA2+OB2=AB2ЃЌЕУЃК(m2+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
ЛЏМђЃЌЕУmn=4ЃЎ
БОД№АИНіЙЉВЮПМЃЌШєгаЦфЫћНтЗЈЃЌЧыВЮееБОЦРЗжБъзМЦРЗжЃЎ
ЕуЦРЃКБОЬтзХжиПМВщСЫХзЮяЯпЕФЖдГЦадКЭЯрЫЦШ§НЧаЮЕФХаЖЈКЭаджЪЃЌЕкЃЈ3ЃЉЮЪЧѓГіmn=4ЪЧНтЬтЕФЙиМќЃЌзлКЯадНЯЧПЃЌгавЛЖЈЕФФбЖШЃЎ

СЗЯАВсЯЕСаД№АИ
 Ш§аТПьГЕН№ХЦжмжмСЗЯЕСаД№АИ
Ш§аТПьГЕН№ХЦжмжмСЗЯЕСаД№АИ
ЯрЙиЬтФП

 ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ
ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ
 ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ
ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ
 ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ
ЃЈШчЭМ1ЃЉЃЌЧѓaЕФжЕЃЛ