题目内容
 如图,直径AB、CD互相垂直,P为
如图,直径AB、CD互相垂直,P为 |
| BC |
求证:
| CP+DP |
| BP+AP |
| AP |
| DP |
分析:连AC,AD,BD,将△ACP绕A点顺时针旋转90°,使AC与AD重合(依AB⊥CD知AC=AD)点P旋转到Q点,可证得△APQ是等腰直角三角形,CP+DP=
AP,同理可得BP+AP=
DP,继而可证得结论.
| 2 |
| 2 |
解答::解:连AC,AD,BD,将△ACP绕A点顺时针旋转90°,使AC与AD重合(依AB⊥CD知AC=AD)点P旋转到Q点,
∴AQ=AP,CP=QD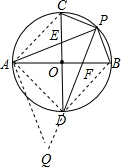 ,
,
∵∠PAQ=90°,AQ=AP,
∵∠ADQ+∠ADP=∠ACP+∠ADP=180°,
∴P,D,Q三点共线,
∴∠Q=∠APD=45°,
∴PQ2=PA2+AQ2,
∴PQ=
AP,
即CP+DP=
AP,
同理:BP+AP=
DP,
∴
=
.
∴AQ=AP,CP=QD
 ,
,∵∠PAQ=90°,AQ=AP,
∵∠ADQ+∠ADP=∠ACP+∠ADP=180°,
∴P,D,Q三点共线,
∴∠Q=∠APD=45°,
∴PQ2=PA2+AQ2,
∴PQ=
| 2 |
即CP+DP=
| 2 |
同理:BP+AP=
| 2 |
∴
| CP+DP |
| BP+AP |
| AP |
| DP |
点评:此题考查了圆周角定理、垂径定理、旋转的性质以及勾股定理.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 如图,直径AB、CD互相垂直,现有一小球在此圆盘上滚动,落在阴影部分的概率为( )
如图,直径AB、CD互相垂直,现有一小球在此圆盘上滚动,落在阴影部分的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,直径AB、CD相互垂直,P为
如图,直径AB、CD相互垂直,P为 如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长. 如图,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=60°,则CD的长为
如图,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=60°,则CD的长为