题目内容
 如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.分析:过O作OF垂直于CD,连接OD,利用垂径定理得到F为CD的中点,由AE+EB求出直径AB的长,进而确定出半径OA与OD的长,由OA-AE求出OE的长,在直角三角形OEF中,利用30°所对的直角边等于斜边的一半求出OF的长,在直角三角形ODF中,利用勾股定理求出DF的长,由CD=2DF即可求出CD的长.
解答: 解:过O作OF⊥CD,交CD于点F,连接OD,
解:过O作OF⊥CD,交CD于点F,连接OD,
∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA-AE=4-2=2,
在Rt△OEF中,∠DEB=30°,
∴OF=
OE=1,
在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF=
=
,
则CD=2DF=2
.
 解:过O作OF⊥CD,交CD于点F,连接OD,
解:过O作OF⊥CD,交CD于点F,连接OD,∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA-AE=4-2=2,
在Rt△OEF中,∠DEB=30°,
∴OF=
| 1 |
| 2 |
在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF=
| OD2-OF2 |
| 15 |
则CD=2DF=2
| 15 |
点评:此题考查了垂径定理,勾股定理,以及含30°直角三角形的性质,利用了转化的思想,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
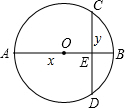 图中的弦CD的长度,通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式
图中的弦CD的长度,通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式


