题目内容
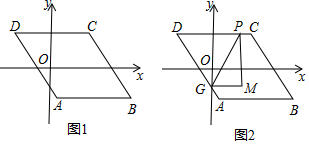
3.如图1,已知?ABCD,AB∥x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是?ABCD边上的一个动点.(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标.(直接写出答案)
分析 (1)由题意点P与点C重合,可得点P坐标为(3,4);
(2)分两种情形①当点P在边AD上时,②当点P在边AB上时,分别列出方程即可解决问题;
(3)分三种情形①如图1中,当点P在线段CD上时.②如图2中,当点P在AB上时.③如图3中,当点P在线段AD上时.分别求解即可;
解答 解:(1)∵CD=6,
∴点P与点C重合,
∴点P坐标为(3,4).
(2)①当点P在边AD上时,
∵直线AD的解析式为y=-2x-2,
设P(a,-2a-2),且-3≤a≤1,
若点P关于x轴的对称点Q1(a,2a+2)在直线y=x-1上,
∴2a+2=a-1,
解得a=-3,
此时P(-3,4).
若点P关于y轴的对称点Q3(-a,-2a-2)在直线y=x-1上时,
∴-2a-2=-a-1,解得a=-1,此时P(-1,0)
②当点P在边AB上时,设P(a,-4)且1≤a≤7,
若等P关于x轴的对称点Q2(a,4)在直线y=x-1上,
∴4=a-1,解得a=5,此时P(5,-4),
若点P关于y轴的对称点Q4(-a,-4)在直线y=x-1上,
∴-4=-a-1,
解得a=3,此时P(3,-4),
综上所述,点P的坐标为(-3,4)或(-1,0)或(5,-4)或(3,-4).
(3)①如图1中,当点P在线段CD上时,设P(m,4).
在Rt△PNM′中,∵PM=PM′=6,PN=4,
∴NM′=$\sqrt{M′{P}^{2}-P{N}^{2}}$=2$\sqrt{5}$,
在Rt△OGM′中,∵OG2+OM′2=GM′2,
∴22+(2$\sqrt{5}$+m)2=m2,
解得m=-$\frac{6\sqrt{5}}{5}$,
∴P(-$\frac{6\sqrt{5}}{5}$,4)
根据对称性可知,P($\frac{6\sqrt{5}}{5}$,4)也满足条件.
②如图2中,当点P在AB上时,易知四边形PMGM′是正方形,边长为2,此时P(2,-4).
③如图3中,当点P在线段AD上时,设AD交x轴于R.易证∠M′RG=∠M′GR,推出M′R=M′G=GM,设M′R=M′G=GM=x.
∵直线AD的解析式为y=-2x-2,
∴R(-1,0),
在Rt△OGM′中,有x2=22+(x-1)2,解得x=$\frac{5}{2}$,
∴P(-$\frac{5}{2}$,3).
点P坐标为(2,-4)或(-$\frac{5}{2}$,3)或(-$\frac{6\sqrt{5}}{5}$,4)或($\frac{6\sqrt{5}}{5}$,4).
点评 本题考查一次函数综合题、平行四边形的性质、翻折变换、勾股定理、正方形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考压轴题.

| A. | x为有理数 | B. | x≠0 | C. | x≠6 | D. | x≠-6 |
| A. | 74.4×1012 | B. | 7.44×1012 | C. | 0.744×1013 | D. | 7.44×1013 |
| A. | 方程2x-1=x+5移项,得2x+x=5+1 | |
| B. | 方程$\frac{x}{2}$+$\frac{x}{3}$=1去分母,得3x+2x=1 | |
| C. | 方程-7x=4系数化为1,得x=-$\frac{7}{4}$ | |
| D. | 方程(x+2)-2(x-1)=0去括号,得x+2-2x+2=0 |
| A. | 无解 | B. | x=1 | C. | x=-1 | D. | x=±1 |
| A. | 亏损20元 | B. | 盈利20元 | C. | 亏损80元 | D. | 盈利80元 |
| A. | a2+a2=a4 | B. | a2•a3=a6 | C. | (-2a2)3=8a6 | D. | (ab)2=a2b2 |
| A. | 事件A和B都是随机事件 | B. | 只有事件B是随机事件 | ||
| C. | 只有事件A是随机事件 | D. | 事件A和B都不是随机事件 |