题目内容
若⊙O是△ABC的外接圆，OD⊥BC于D，且∠BOD=48°，∠BAC=________．
48°或132°
分析：连接OC，根据垂径定理可知：∠BOC=2∠BOD=96°，由于△ABC可能是锐角三角形，也可能是钝角三角形，因此分类讨论即可．
解答：
解：连接OC，则∠BOC=2∠BOD=96°，
①当△ABC是锐角三角形时，∠A=
∠BOC=48°；
②当△ABC是钝角三角形时，∠A=180°-48°=132°．
因此∠BAC的度数为48°或132°．
点评：本题主要考查了圆周角定理、全等三角形的判定和性质、垂径定理、圆内接四边形的性质等知识．
分析：连接OC，根据垂径定理可知：∠BOC=2∠BOD=96°，由于△ABC可能是锐角三角形，也可能是钝角三角形，因此分类讨论即可．
解答：
解：连接OC，则∠BOC=2∠BOD=96°，①当△ABC是锐角三角形时，∠A=
∠BOC=48°；②当△ABC是钝角三角形时，∠A=180°-48°=132°．
因此∠BAC的度数为48°或132°．
点评：本题主要考查了圆周角定理、全等三角形的判定和性质、垂径定理、圆内接四边形的性质等知识．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
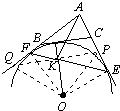9、如图，⊙O是△ABC的边BC外的旁切圆，D、E、F分别为⊙O与BC、CA、AB的切点．若OD与EF相交于K，求证：AK平分BC．
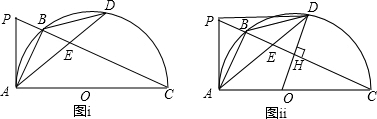与H，BE=2，EC=4，连接PD，请探究四边形ABDO是什么特殊的四边形，并求tan∠DPC的值．
