题目内容
 如图.设BC是△ABC的最长边,在此三角形内部任选一点O,AO,BO,CO分别交对边于A′,B′,C′.
如图.设BC是△ABC的最长边,在此三角形内部任选一点O,AO,BO,CO分别交对边于A′,B′,C′.证明:(1)OA′+OB′+OC′<BC;
(2)OA′+OB′+OC′≤max{AA′,BB′,CC′}.
分析:过点O作OX,OY分别平行于边AB,AC,交边BC于X,Y点,再过X,Y分别作XS,YT平行于CC′和BB′交AB,AC于S,T.由于△OXY∽△ABC,所以XY是△OXY的最大边,所以OA′<max{OX,OY}≤XY.同理可求BX>XS=OC′,CY>OB′.
解答:证明:(1)过点O作OX,OY分别平行于边AB,AC,交边BC于X,Y点,再过X,Y分别作XS,YT平行于CC′和BB′交AB,AC于S,T,由于△OXY∽△ABC,所以XY是△OXY的最大边,所以OA′<max{OX,OY}≤XY,
又△BXS∽△BCC′,而BC是△BCC′中的最大边,从而BX也是△BXS中的最大边,而且SXOC′是平行四边形,
所以BX>XS=OC′,
同理CY>OB′,
所以OA′+OB′+OC′<XY+BX+CY=BC,
=x,
=y,
=z,
由于x+y+z=
+
+
=1,
所以OA′+OB′+OC′=x•AA′+y•BB′+z•CC′,
≤(x+y+z)max{AA′,BB′,CC′},
=max{AA′,BB′,CC′}.
又△BXS∽△BCC′,而BC是△BCC′中的最大边,从而BX也是△BXS中的最大边,而且SXOC′是平行四边形,
所以BX>XS=OC′,
同理CY>OB′,
所以OA′+OB′+OC′<XY+BX+CY=BC,
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
由于x+y+z=
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
所以OA′+OB′+OC′=x•AA′+y•BB′+z•CC′,
≤(x+y+z)max{AA′,BB′,CC′},
=max{AA′,BB′,CC′}.
点评:本题考查相似三角形的判定和性质以及作出适当的辅助线求解,本题的关键是作OX,OY分别平行于边AB,AC,交边BC于X,Y点,再过X,Y分别作XS,YT平行于CC′和BB′交AB,AC于S,T.

练习册系列答案
相关题目
 如图,设△ABC是直角三角形,点D在斜边BC上,BD=4DC.已知圆过点C且与AC相交于F,与AB相切于AB的中点G.求证:AD⊥BF.
如图,设△ABC是直角三角形,点D在斜边BC上,BD=4DC.已知圆过点C且与AC相交于F,与AB相切于AB的中点G.求证:AD⊥BF.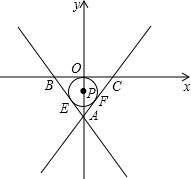
 如图,设P是△ABC内任一点,AD,BE,CF是过点P且分别交边BC,CA,AB于D,E,F.
如图,设P是△ABC内任一点,AD,BE,CF是过点P且分别交边BC,CA,AB于D,E,F.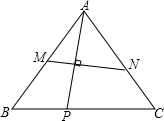 如图,设P是等边△ABC的一边BC上的任意一点,连接AP,它的垂直平分线交AB、AC于M、N两点,求证:BP•PC=BM•CN.
如图,设P是等边△ABC的一边BC上的任意一点,连接AP,它的垂直平分线交AB、AC于M、N两点,求证:BP•PC=BM•CN. 如图,设P是凸四边形ABCD内的一点,过P分别作AB、BC、CD、DA的垂线,垂足分别为E、F、G、H.已知AH=3,HD=4,DG=1,GC=5,CF=6,FB=4,且BE-AE=1.则四边形ABCD的周长为
如图,设P是凸四边形ABCD内的一点,过P分别作AB、BC、CD、DA的垂线,垂足分别为E、F、G、H.已知AH=3,HD=4,DG=1,GC=5,CF=6,FB=4,且BE-AE=1.则四边形ABCD的周长为