Question

13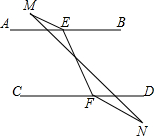．如图所示，AB∥CD，点E、F分别在AB、CD上，若∠MEA=∠NFD，求证：∠M=∠N（请注明每一步的推理依据）．

Answer 1

分析 先根据平行线的性质以及∠MEA=∠NFD，得出∠MEF=∠NFE，进而判定ME∥NF，根据平行线的性质，即可得出∠M=∠N．

解答 证明：∵AB∥CD，（已知）
∴∠AEF=∠DFE，（两直线平行，内错角相等）
又∵∠MEA=∠NFD，（已知）
∴∠AEF+∠MEA=∠DEF+∠NFD，（等式的基本性质）
即∠MEF=∠NFE，
∴ME∥NF，（内错角相等，两直线平行）
∴∠M=∠N，（两直线平行，内错角相等）

点评 本题主要考查了平行线的性质与判定的运用，平行线的判定是由角的数量关系判断两直线的位置关系；平行线的性质是由平行关系来寻找角的数量关系．