题目内容
从数-2,-1,1,2,3中任取两个,其和的绝对值为k(k是自然数)的概率记作Pk.(如:P4是任取两个数,其和的绝对值为4的概率)
(1)求k的所有取值;
(2)求P3;
(3)能否找到概率Pi,Pj,Pm,Pn(0≤i<j<m<n),使得Pi+Pj+Pm+Pn=0.5?,若能找到,请举例说明;若不能找到,请说明理由.
(1)求k的所有取值;
(2)求P3;
(3)能否找到概率Pi,Pj,Pm,Pn(0≤i<j<m<n),使得Pi+Pj+Pm+Pn=0.5?,若能找到,请举例说明;若不能找到,请说明理由.
考点:列表法与树状图法
专题:
分析:(1)首先根据题意列出表格,然后由表格即可求得所有等可能的结果;
(2)根据(1)中的表格即可得共有20种等可能的结果,其和的绝对值为3的有4种情况,然后利用概率公式求解即可求得答案;
(3)首先根据表格求得各种情况的概率,继而求得答案.
(2)根据(1)中的表格即可得共有20种等可能的结果,其和的绝对值为3的有4种情况,然后利用概率公式求解即可求得答案;
(3)首先根据表格求得各种情况的概率,继而求得答案.
解答:解:(1)列表得:
由表可知一共有20种情况,k的所有取值分别为:0,1,2,3,4,5;
(2)∵共有20种等可能的结果,其和的绝对值为3的有4种情况,
∴P3=
=
;
(3)能找到.
∵由表格得:P0=P3=
=
,P1=
=
,P2=P4=P5=
=
,
∴P0+P2+P4+P5=0.5,P2+P3+P4+P5=0.5.
| 3 | 1 | 2 | 4 | 5 | |
| 2 | 0 | 1 | 3 | 5 | |
| 1 | 1 | 0 | 3 | 4 | |
| -1 | 3 | 0 | 1 | 2 | |
| -2 | 3 | 1 | 0 | 1 | |
| -2 | -1 | 1 | 2 | 3 |
(2)∵共有20种等可能的结果,其和的绝对值为3的有4种情况,
∴P3=
| 4 |
| 20 |
| 1 |
| 5 |
(3)能找到.
∵由表格得:P0=P3=
| 4 |
| 20 |
| 1 |
| 5 |
| 6 |
| 20 |
| 3 |
| 10 |
| 2 |
| 20 |
| 1 |
| 10 |
∴P0+P2+P4+P5=0.5,P2+P3+P4+P5=0.5.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 如图,点A、B、C、D在圆O上,直线AB,CD相交于点P,AQ∥CD,交圆O于点Q,已知
如图,点A、B、C、D在圆O上,直线AB,CD相交于点P,AQ∥CD,交圆O于点Q,已知
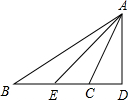 如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于D点,则∠DAE,∠ACB,∠B之间存在何种等量关系?并说明理由.
如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于D点,则∠DAE,∠ACB,∠B之间存在何种等量关系?并说明理由. 如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EF=5,求∠DFE的度数和DE的长.
如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EF=5,求∠DFE的度数和DE的长.