Question

AD是△ABC的中线，已知AB=2n²+2n+1，AC=2n+1，AD=n²+n，则△ABC的面积为

 

（用n的代数式表示）．

Answer 1

分析：延长AD至E，使DE=AD，连接BE．根据全等三角形的性质和勾股定理的逆定理发现三角形ABE是直角三角形，进而求得三角形的面积．

解答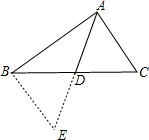：解：延长AD至E，使DE=AD，连接BE．
∵BD=CD，DE=AD，∠ADC=∠BDE，
∴△ACD≌△EBD，
∴BE=AC=2n+1．
∵AB²=（2n²+2n）²+2（2n²+2n）+1，BE²=（2n+1）²，AE²=（2n²+2n）²，
∴AB²=AE²+BE²，
∴∠AEB=90°．
∴△ABC的面积=△ABE的面积=

1

2

AE•BE=（n²+n）（2n+1）．
故答案为（n²+n）（2n+1）．

点评：此题综合考查了全等三角形的判定和性质以及勾股定理的逆定理．
注意：倍长中线是常见的辅助线之一．