题目内容
试证明:不论x,y为何值,x2+y2+x-y+1的值都为正数.
分析:原式配方后,利用完全平方式大于等于0即可得证.
解答:证明:x2+y2+x-y+1=(x+
)2+(y-
)2+
≥
>0,
则不论x,y为何值,x2+y2+x-y+1的值都为正数.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则不论x,y为何值,x2+y2+x-y+1的值都为正数.
点评:此题考查了配方法的应用,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
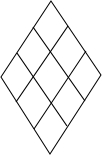 北京101中学的学生为迎接2008年奥运会,美化校园,在周长为12m,夹角为60°的菱形花坛里栽十株花.试证明:不论如何安排,至少有两株花的距离小于
北京101中学的学生为迎接2008年奥运会,美化校园,在周长为12m,夹角为60°的菱形花坛里栽十株花.试证明:不论如何安排,至少有两株花的距离小于 北京101中学的学生为迎接2008年奥运会,美化校园,在周长为12m,夹角为60°的菱形花坛里栽十株花.试证明:不论如何安排,至少有两株花的距离小于
北京101中学的学生为迎接2008年奥运会,美化校园,在周长为12m,夹角为60°的菱形花坛里栽十株花.试证明:不论如何安排,至少有两株花的距离小于 m.
m.