题目内容
10.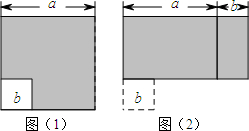 如图,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由如图(1)中阴影部分拼成的一个长方形.
如图,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由如图(1)中阴影部分拼成的一个长方形.(1)请你分别表示图中阴影部分的面积
(2)以上结果可验证哪个乘法公式
(3)试利用这个公式计算:(2+1)(22+1)(24+1)…(28+1)+1.
分析 (1)求出大正方形及小正方形的面积,作差即可得出阴影部分的面积;图2所示的长方形的长和宽分别为(a+b)、(a-b),由此可计算出面积;
(2)根据阴影部分的面积相等可得出平方差公式;
(3)利用平方差公式计算即可.
解答 解:(1)大正方形的面积为a2,小正方形的面积为b2,
故图(1)阴影部分的面积值为a2-b2;
长方形的长和宽分别为(a+b)、(a-b),
故图(2)重拼的长方形的面积为(a+b)(a-b);
(2)比较上面的结果,都表示同一阴影的面积,它们相等,
即a2-b2=(a+b)(a-b),可以验证平方差公式,这也是平方差公式的几何意义;
(3)(2+1)(22+1)(24+1)…(28+1)+1
=(22-1)(22+1)(24+1)…(28+1)+1
=216-1+1
=216.
点评 本题考查了平方差公式的几何背景,注意几次分割后边的变化情况是关键,属于基础题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
3.计算:$\sqrt{\frac{5}{3}}$÷$\sqrt{\frac{1}{3}}$的结果是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 5 | D. | $\frac{\sqrt{5}}{3}$ |
20.若2m-3与6-m是某个正数的平方根,则m的值为( )
| A. | -3 | B. | 3 | C. | ±3 | D. | ±9 |
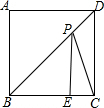 如图,在正方形ABCD中,点E在BC上,BE=6,CE=2,点P是BD上的一个动点(不包括B、D两点),则PE和PC的长度和的最小值为10.
如图,在正方形ABCD中,点E在BC上,BE=6,CE=2,点P是BD上的一个动点(不包括B、D两点),则PE和PC的长度和的最小值为10.

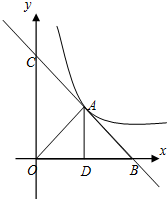 如图,一次函数的图象与反比例函数的图象在第一象限只有-个交点A,一次函数的图象与x轴、y轴分别交于B、C 两点,AD垂直平分OB,垂足为D,OA=$\sqrt{13}$,cos∠ABO=$\frac{{2\sqrt{13}}}{13}$.
如图,一次函数的图象与反比例函数的图象在第一象限只有-个交点A,一次函数的图象与x轴、y轴分别交于B、C 两点,AD垂直平分OB,垂足为D,OA=$\sqrt{13}$,cos∠ABO=$\frac{{2\sqrt{13}}}{13}$.