题目内容
若抛物线y1=a1x2+b1x+c1与y2=a2x2+b2x+c2满足
=
=
=k(k≠0,1),则称y1,y2互为“相关抛物线”.给出如下结论:
①y1与y2的开口方向,开口大小不一定相同;
②y1与y2的对称轴相同;
③若y2的最值为m,则y1的最值为k2m;
④若y2与x轴的两交点间距离为d,则y1与x轴的两交点间距离也为d.
其中正确的结论的序号是
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
①y1与y2的开口方向,开口大小不一定相同;
②y1与y2的对称轴相同;
③若y2的最值为m,则y1的最值为k2m;
④若y2与x轴的两交点间距离为d,则y1与x轴的两交点间距离也为d.
其中正确的结论的序号是
①②④
①②④
(把所有正确结论的序号都填在横线上).分析:根据相关抛物线的条件,a1、a2的符号不一定相同,即可得到开口方向、开口大小不一定相同,代入对称轴-
和
即可判断②、③,根据根与系数的关系求出与x轴的两交点的距离|g-e|和|d-m|,即可判断④.
| b |
| 2a |
| 4ac-b2 |
| 4a |
解答:解:由已知可知:a1=ka2,b1=kb2,c1=kc2,
①根据相关抛物线的条件,a1、a2的符号不一定相同,所以开口方向、开口大小不一定相同,故本选项错误;
②因为
=
=k,代入-
得到对称轴相同,故本选项错误;
③因为如果y2的最值是m,则y1的最值是
=k•
=km,故本选项错误;
④因为设抛物线y1与x轴的交点坐标是(e,0),(g,0),则e+g=-
,eg=
,抛物线y2与x轴的交点坐标是(m,0),(d,0),则m+d=-
,md=
,可求得:|g-e|=|d-m|=
,故本选项正确.
故答案为:①②④.
①根据相关抛物线的条件,a1、a2的符号不一定相同,所以开口方向、开口大小不一定相同,故本选项错误;
②因为
| a1 |
| a2 |
| b1 |
| b2 |
| b |
| 2a |
③因为如果y2的最值是m,则y1的最值是
4a1c1-
| ||
| 4a1 |
4a2c2-
| ||
| 4a2 |
④因为设抛物线y1与x轴的交点坐标是(e,0),(g,0),则e+g=-
| b1 |
| a1 |
| c1 |
| a1 |
| b2 |
| a2 |
| c2 |
| a2 |
|
故答案为:①②④.
点评:本题主要考查了二次函数图象上点的坐标特征,抛物线与x轴的交点,二次函数的最值等知识点解此题的关键是能根据相关抛物线的条件进行判断.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
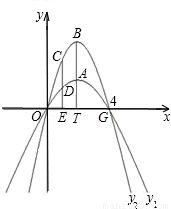
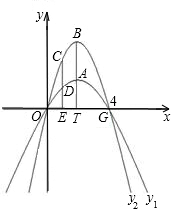 经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.
经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.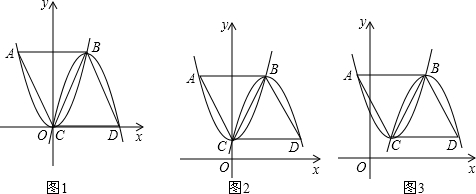
 经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.
经过原点和G(4,0)的两条抛物线y1=a1x2+b1x,y2=a2x2+b2x,顶点分别为A,B,且都在第1象限,连接BA交x轴于T,且BA=AT=3.