题目内容
如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE=9，则两平行线AD与BC间的距离为考点：角平分线的性质,平行线之间的距离
专题：
分析：根据角平分线的性质以及平行线的性质即可得出PM=PE=2，PE=PN=2，即可得出答案．
解答：
解：过点P作MN⊥AD，
∵AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，PE⊥AB于点E，
∴AP⊥BP，PN⊥BC，
∴PM=PE=9，PE=PN=9，
∴MN=9+9=18．
故答案为：18．
解：过点P作MN⊥AD，∵AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，PE⊥AB于点E，
∴AP⊥BP，PN⊥BC，
∴PM=PE=9，PE=PN=9，
∴MN=9+9=18．
故答案为：18．
点评：本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．
练习册系列答案
相关题目
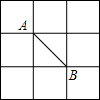如图，A，B是3×3的正方形网格中的两个格点，C也是网格中的一个格点，连接AC、BC，当△ABC为等腰三角形时，格点C的不同位置有（ ）| A、5个 | B、6个 | C、7个 | D、8个 |
如图，为抄近路践踏草坪是一种不文明的现象，请你用数学知识解释出“人们喜欢抄近路”这一现象的原因是
将一张等宽的直角形纸片按图中的方式折叠，若∠1=36°，则∠2的度数为对于一次函数y=kx-k（k≠0），下列叙述正确的是（ ）
| A、当k＞0时，函数图象经过第一、二、三象限 |
| B、当k＞0时，y随x的增大而减小 |
| C、当k＜0时，函数图象一定交于y轴负半轴一点 |
| D、函数图象一定经过点（1，0） |
画出如图所示的几何体的三种视图．如果分式
的值为0，那么x等于（ ）
| |x|-1 |
| x2-5x+4 |
| A、-1 | B、1 |
| C、-1或1 | D、1或2 |