题目内容
 如图,一次函数y=kx+b交两轴于A、B两点,M(-1,0),AM=
如图,一次函数y=kx+b交两轴于A、B两点,M(-1,0),AM=| 10 |
(1)求一次函数的解析式;
(2)求四边形PMOC的面积;
(3)过N作NC⊥AM于C,求证:PN=
| 2 |
考点:一次函数综合题
专题:计算题
分析:(1)由M的坐标得到OM的长,在直角三角形AOM中,由OM与AM的长,利用勾股定理求出OA的长,确定出A的坐标,由BM=AO求出BM的长,再由BM+OM求出OB的长,确定出B的坐标,将A与B坐标代入一次函数y=kx+b中求出k与b的值,即可确定出一次函数解析式;
(2)四边形PMON的面积=三角形BON面积-三角形BPM面积,由AN=OM求出AN的长,再由OA-AN求出ON的长,确定出N坐标,由OB与ON长求出三角形BON面积,设直线BN解析式为y=mx+n,将N与B坐标代入求出m与n的值,确定出直线BN解析式,同理确定出直线AM解析式,联立两解析式求出交点P的坐标,由BM与P纵坐标的绝对值求出三角形BMP的面积,进而求出四边形PMON的面积;
(3)过N作NC⊥AM,过M作MQ⊥BN,由P与B坐标利用两点间的距离公式求出BP的长,再由(2)求出的三角形BPM的面积,利用面积公式求出BP边上高MQ的长,在直角三角形BMQ中,由BM与MQ的长,利用勾股定理求出BQ的长,由BP-BQ求出PQ的长,发现PQ=MQ,可得出三角形PQM为等腰直角三角形,再根据对顶角相等得到∠CPN=∠QOM=45°,在直角三角形CPN中,利用锐角三角函数定义及特殊角的三角函数值化简,即可得证.
(2)四边形PMON的面积=三角形BON面积-三角形BPM面积,由AN=OM求出AN的长,再由OA-AN求出ON的长,确定出N坐标,由OB与ON长求出三角形BON面积,设直线BN解析式为y=mx+n,将N与B坐标代入求出m与n的值,确定出直线BN解析式,同理确定出直线AM解析式,联立两解析式求出交点P的坐标,由BM与P纵坐标的绝对值求出三角形BMP的面积,进而求出四边形PMON的面积;
(3)过N作NC⊥AM,过M作MQ⊥BN,由P与B坐标利用两点间的距离公式求出BP的长,再由(2)求出的三角形BPM的面积,利用面积公式求出BP边上高MQ的长,在直角三角形BMQ中,由BM与MQ的长,利用勾股定理求出BQ的长,由BP-BQ求出PQ的长,发现PQ=MQ,可得出三角形PQM为等腰直角三角形,再根据对顶角相等得到∠CPN=∠QOM=45°,在直角三角形CPN中,利用锐角三角函数定义及特殊角的三角函数值化简,即可得证.
解答:(1)解:由M(-1,0),得到OM=1,
在Rt△AOM中,OM=1,AM=
,
根据勾股定理得:AO=
=3,
∴A(0,3),
又∵AO=BM=3,OM=1,
∴OB=OM+MB=4,即B(-4,0),
将A与B坐标代入y=kx+b中得:
,
解得:
,
则一次函数解析式为y=
x+3;
(2)解:∵AN=OM=1,OA=3,
∴ON=3-1=2,即N(0,2),
设直线BN解析式为y=mx+n,将N与B坐标代入得:
,
解得:
,
则直线BN解析式为y=
x+2,
同理直线AM解析式为y=3x+3,
联立两解析式得:
,
解得:
,即P(-
,
),
则S四边形PMON=S△BON-S△BMP=
OB•ON-
BM•|yP纵坐标|=
×4×2-
×3×
=
;
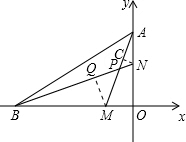 (3)证明:过N作NC⊥AM,过M作MQ⊥BN,如图所示,
(3)证明:过N作NC⊥AM,过M作MQ⊥BN,如图所示,
∵P(-
,
),B(-4,0),
∴BP=
=
,
∴S△BMP=
BP•QM=
×
×QM=
×3×
,即QM=
,
在Rt△BMQ中,BM=3,QM=
,
根据勾股定理得:BQ=
=
,
则PQ=BP-BQ=
-
=
=QM,
∴△PQM为等腰直角三角形,
∴∠QPM=45°,
∴∠CPN=∠QOM=45°,又∠PCN=90°,
∴sin∠CPN=sin45°=
=
,
则PN=
NC.
在Rt△AOM中,OM=1,AM=
| 10 |
根据勾股定理得:AO=
| AM2-OM2 |
∴A(0,3),
又∵AO=BM=3,OM=1,
∴OB=OM+MB=4,即B(-4,0),
将A与B坐标代入y=kx+b中得:
|
解得:
|
则一次函数解析式为y=
| 3 |
| 4 |
(2)解:∵AN=OM=1,OA=3,
∴ON=3-1=2,即N(0,2),
设直线BN解析式为y=mx+n,将N与B坐标代入得:
|
解得:
|
则直线BN解析式为y=
| 1 |
| 2 |
同理直线AM解析式为y=3x+3,
联立两解析式得:
|
解得:
|
| 2 |
| 5 |
| 9 |
| 5 |
则S四边形PMON=S△BON-S△BMP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 5 |
| 13 |
| 10 |
 (3)证明:过N作NC⊥AM,过M作MQ⊥BN,如图所示,
(3)证明:过N作NC⊥AM,过M作MQ⊥BN,如图所示,∵P(-
| 2 |
| 5 |
| 9 |
| 5 |
∴BP=
(-
|
9
| ||
| 5 |
∴S△BMP=
| 1 |
| 2 |
| 1 |
| 2 |
9
| ||
| 5 |
| 1 |
| 2 |
| 9 |
| 5 |
3
| ||
| 5 |
在Rt△BMQ中,BM=3,QM=
3
| ||
| 5 |
根据勾股定理得:BQ=
| BM2-QM2 |
6
| ||
| 5 |
则PQ=BP-BQ=
9
| ||
| 5 |
6
| ||
| 5 |
3
| ||
| 5 |
∴△PQM为等腰直角三角形,
∴∠QPM=45°,
∴∠CPN=∠QOM=45°,又∠PCN=90°,
∴sin∠CPN=sin45°=
| NC |
| PN |
| ||
| 2 |
则PN=
| 2 |
点评:此题考查了一次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,两直线的交点坐标,两点间的距离公式,等腰直角三角形的判定与性质,勾股定理,坐标与图形性质,锐角三角函数定义,以及特殊角的三角函数值,灵活运用待定系数法是解本题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
如果把分式
中的x、y同时扩大为原来的3倍,则分式的值( )
| x |
| x+y |
| A、不变 | ||
| B、是原来的3倍 | ||
C、是原来的
| ||
D、是原来的
|
下列有理数2,-
,0,-3中,最小的数是( )
| 1 |
| 2 |
A、-
| ||
| B、0 | ||
| C、2 | ||
| D、-3 |
若(x+y-2)2+|4x+3y-7|=0,则x+y的值为( )
| A、0 | B、1 | C、2 | D、3 |
 如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由.
如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由.