题目内容
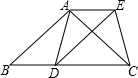（2013•北塘区一模）如图，在△ABC中，AB=AC，D为边BC上一点，以AB、BD为邻边作?ABDE，连接AD、EC．求证：AD=EC．分析：利用等边对等角以及平行四边形的性质可以证得∠EDC=∠ACB，则易证△ADC≌△ECD，利用全等三角形的对应边相等即可证得．
解答：证明：∵AB=AC，
∴∠B=∠ACB，
又∵?ABDE中，AB=DE，AB∥DE，
∴∠B=∠EDC=∠ACB，AC=DE，
∴在△ADC和△ECD中，
，
∴△ADC≌△ECD．
∴AD=EC．
∴∠B=∠ACB，
又∵?ABDE中，AB=DE，AB∥DE，
∴∠B=∠EDC=∠ACB，AC=DE，
∴在△ADC和△ECD中，
|
∴△ADC≌△ECD．
∴AD=EC．
点评：本题考查了平行四边形的性质以及等腰三角形的性质、全等三角形的判定与性质，证明两线段相等常用的方法就是转化为证两三角形全等．
练习册系列答案
相关题目
（2013•北塘区一模）如图，在Rt△ABC中，D、E分别是AC、AB的中点，DE=1.5，CE=2.5，则AC=