Question

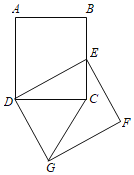
【题目】如图，在矩形ABCD中，AB＝15，BC＝17，将矩形ABCD绕点D按顺时针方向旋转得到矩形DEFG，点A落在矩形ABCD的边BC上，连接CG，则CG的长是_____．

Answer 1

【答案】

【解析】

连接AE，由旋转变换的性质可知，∠ADE＝∠CDG，AD＝BC＝DE＝17，AB＝CD＝DG＝15，由勾股定理得，CE＝，得出BE＝BCCE＝9，则AE＝，进一步证明△ADE∽△CDG，得出，然后即可得出结果．

连接AE，如图所示：

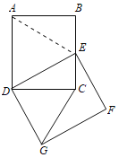
由旋转变换的性质可知，∠ADE＝∠CDG，AD＝BC＝DE＝17，AB＝CD＝DG＝15，

由勾股定理得，CE＝，

∴BE＝BC﹣CE＝17﹣8＝9，

则AE，

∵，∠ADE＝∠CDG，

∴△ADE∽△CDG，

∴，

解得，CG＝，

故答案为：．