已知∠AOB=60°.点P是∠AOB的平分线OC上的动点.点M在边OA上.且OM=4.则点P到点M与到边OA的距离之和的最小值是2$\sqrt{3}$．题目和参考答案——青夏教育精英家教网—

题目内容

8．已知∠AOB=60°，点P是∠AOB的平分线OC上的动点，点M在边OA上，且OM=4，则点P到点M与到边OA的距离之和的最小值是2$\sqrt{3}$．

分析过M作MN′⊥OB于N′，交OC于P，即MN′的长度等于点P到点M与到边OA的距离之和的最小值，解直角三角形即可得到结论．

解答解：过M作MN′⊥OB于N′，交OC于P，
则MN′的长度等于PM+PN的最小值，
即MN′的长度等于点P到点M与到边OA的距离之和的最小值，
∵∠ON′M=90°，OM=4，
∴MN′=OM•sin60°=2$\sqrt{3}$，
∴点P到点M与到边OA的距离之和的最小值为2$\sqrt{3}$．

点评本题考查了轴对称-最短路线问题，解直角三角形，正确的作出图形是解题的关键．

练习册系列答案

相关题目

18．计算：（x-3）（x+4）的结果是x²+x-12．

19．

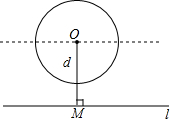如图，给定一个半径长为2的圆，圆心O到水平直线l的距离为d，即OM=d．我们把圆上到直线l的距离等于1的点的个数记为m．如d=0时，l为经过圆心O的一条直线，此时圆上有四个到直线l的距离等于1的点，即m=4，由此可知：
（1）当d=3时，m=1；
（2）当m=2时，d的取值范围是1＜d＜3．

16．

如图，正方形ABCD中，以对角线AC为一边作菱形AEFC，则∠FAB=22.5°．

3．下列结论错误的是（　　）

	A．	对角线相等的菱形是正方形
	B．	对角线互相垂直的矩形是正方形
	C．	对角线互相垂直且相等的四边形是正方形
	D．	对角线互相垂直且相等的平行四边形是正方形

13．每年5月的第二周为“职业教育活动周”，今年我省开展了以“弘扬工匠精神，打造技能强国”为主题的系列活动．活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动，相关职业技术人员进行了现场演示，活动后该校教务处随机抽取了部分学生进行调查：“你最感兴趣的一种职业技能是什么？”并对此进行了统计，绘制了统计图（均不完整）．请解答以下问题：
（1）补全条形统计图和扇形统计图；
（2）若该校共有1800名学生，请估计该校对“工业设计”最感兴趣的学生有多少人？
（3）要从这些被调查的学生中，随机抽取一人进行访谈，那么正好抽到对“机电维修”最感兴趣的学生的概率是0.13．

20．阅读下面材料：
在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？
小敏在思考问题是，有如下思路：连接AC．

结合小敏的思路作答
（1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由；参考小敏思考问题方法解决以下问题：
（2）如图2，在（1）的条件下，若连接AC，BD．
①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；
②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．

17．如图1，抛物线y=ax²-6x+c与x轴交于点A（-5，0）、B（-1，0），与y轴交于点C（0，-5），点P是抛物线上的动点，连接PA、PC，PC与x轴交于点D．
（1）求该抛物线所对应的函数解析式；
（2）若点P的坐标为（-2，3），请求出此时△APC的面积；
（3）过点P作y轴的平行线交x轴于点H，交直线AC于点E，如图2．
①若∠APE=∠CPE，求证：$\frac{AE}{EC}=\frac{3}{7}$；
②△APE能否为等腰三角形？若能，请求出此时点P的坐标；若不能，请说明理由．

18．

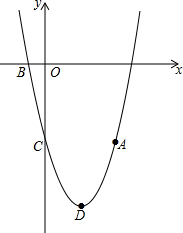如图，抛物线y=ax²+bx-5（a≠0）经过点A（4，-5），与x轴的负半轴交于点B，与y轴交于点C，且OC=5OB，抛物线的顶点为点D．
（1）求这条抛物线的表达式；
（2）连结AB、BC、CD、DA，求四边形ABCD的面积；
（3）如果点E在y轴的正半轴上，且∠BEO=∠ABC，求点E的坐标．

试题分类