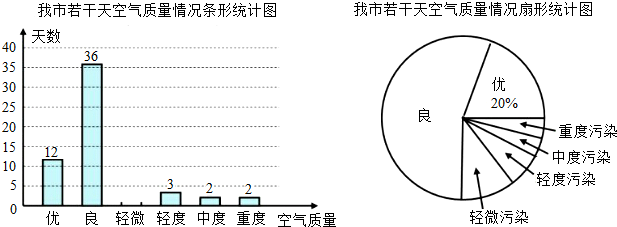
题目内容
5.解方程:(1)2x2=x
(2)x2+4x-1=0(用配方法解)
分析 (1)因式分解法求解可得;
(2)配方法求解可得.
解答 解:(1)∵2x2-x=0,
∴x(2x-1)=0,
则x=0或2x-1=0,
解得:x=0或x=0.5;
(2)∵x2+4x=1,
∴x2+4x+4=1+4,即(x+2)2=5,
则x+2=±$\sqrt{5}$,
∴x=-2±$\sqrt{5}$.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
20.1.996精确到0.01的近似数是( )
| A. | 2 | B. | 2.0 | C. | 1.99 | D. | 2.00 |
15.在△ABC中,a、b、c分别是∠A,∠B,∠C的对边,若(a-1)2+|b-$\sqrt{5}$|+$\sqrt{c-2}$=0,则这个三角形一定是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
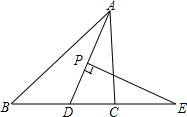 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E,若∠B=35°,∠ACB=85°.
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E,若∠B=35°,∠ACB=85°.