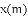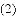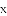��Ŀ����
��ͼ�٣���ֱ��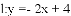
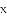
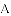
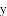
 �õ�
�õ�
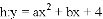 ��
��
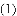
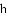
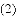
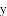
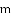
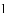
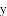
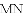
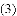
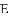
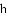
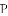
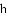
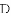
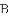
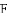
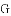
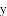
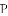
��ϰ��ϵ�д�
�����Ŀ
ijλ�����˶�Ա��ͬ���������½���Ͷ����ϰ��������±���
Ͷ������ |
|
|
|
|
|
|
|
������� |
|
|
|
|
|
|
|
����Ƶ�� | ________ | ________ | ________ | ________ | ________ | ________ | ________ |

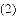



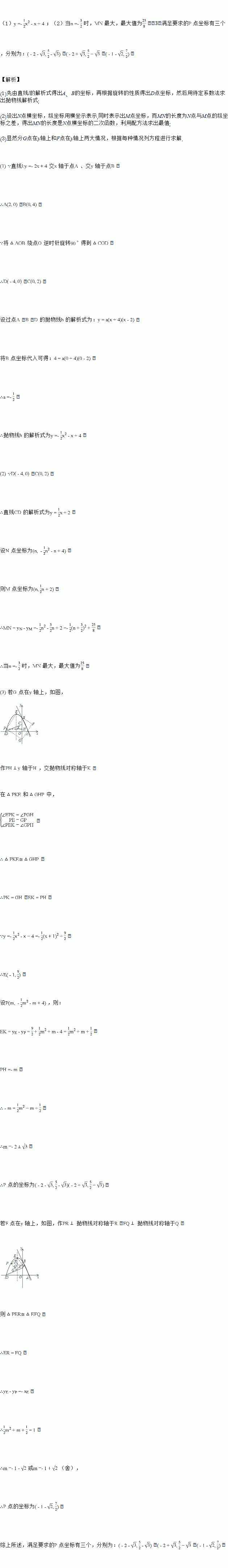



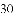


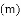




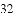


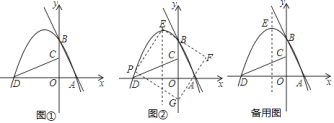
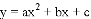 ͼ���һ���֣���Գ���Ϊx=��1���ҹ��㣨��3��0��������˵������abc��0����2a��b=0����4a+2b+c��0����������5��y1������
ͼ���һ���֣���Գ���Ϊx=��1���ҹ��㣨��3��0��������˵������abc��0����2a��b=0����4a+2b+c��0����������5��y1������ ��y2���������������㣬��
��y2���������������㣬��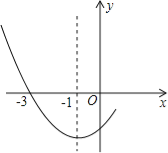
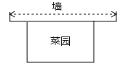
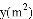 �봹ֱ��ǽ�ı߳�
�봹ֱ��ǽ�ı߳�