题目内容
如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=
 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .


y=2x .
【考点】相似三角形的性质;反比例函数图象上点的坐标特征.
【专题】数形结合.
【分析】设OC=a,根据点D在反比例函数图象上表示出CD,再根据相似三角形对应边成比例列式求出AC,然后根据中点的定义表示出点B的坐标,再根据点B在反比例函数图象上表示出a、k的关系,然后用a表示出点B的坐标,再利用待定系数法求一次函数解析式解答.
【解答】解:设OC=a,
∵点D在y=
 上,
上,
∴CD=
 ,
,
∵△OCD∽△ACO,
∴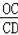
 =
=
 ,
,
∴AC=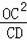
 =
=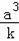
 ,
,
∴点A(a,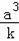
 ),
),
∵点B是OA的中点,
∴点B的坐标为(
 ,
,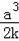
 ),
),
∵点B在反比例函数图象上,
∴
 =
=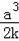
 ,
,
∴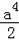
 =2k2,
=2k2,
∴a4=4k2,
解得,a2=2k,
∴点B的坐标为(
 ,a),
,a),
设直线OA的解析式为y=mx,
则m•
 =a,
=a,
解得m=2,
所以,直线OA的解析式为y=2x.
故答案为:y=2x.
【点评】本题考查了相似三角形的性质,反比例函数图象上点的坐标特征,用OC的长度表示出点B的坐标是解题的关键,也是本题的难点.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 ,下列结论错误的是 ( )
,下列结论错误的是 ( )  为两个连续实数,且
为两个连续实数,且 ,则
,则 的值为
的值为  ,则
,则 的值为( )
的值为( ) B、
B、 C、
C、 D、
D、



 B.
B.

 D.
D.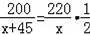



 B.
B.


 ,则代数式
,则代数式 的值为 。
的值为 。 作:分别延长AB,BC,CA至点A1,B1,C1,使
作:分别延长AB,BC,CA至点A1,B1,C1,使 A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操
A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操 作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=
作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=