题目内容
7.如图1,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,AB、EF的中点均为O,连接BF,CD,CO.(1)求证:CD=BF;
(2)如图2,当△DEF绕O点顺时针旋转的过程中,探究BF与CD间的数量关系和位置关系,并证明.

分析 (1)根据等腰直角三角形的性质得CO=BO,OD=OF,则CD=OC+OD=OB+OF=BF;
(2)连结OC、OD,BF与CD相交于H,如图2,根据等腰直角三角形的性质得OC⊥AB,OD⊥EF,则∠BOF=∠DOC,接着可证明△BOF≌△COD得到BF=CD,∠OBF=∠OCD,然后证明∠CHB=∠COB=90°得到BF⊥CD.
解答 解:(1)∵△ABC与△DEF都是等腰直角三角形,
∴AB、EF的中点均为O,
∴CO=BO,OD=OF,
∴CD=OC+OD=OB+OF=BF;
(2)解:BF=CD,BF⊥CD.
理由如下:
连结OC、OD,BF与CD相交于H,如图2,
∵△ABC与△DEF都是等腰直角三角形,
∴OC⊥AB,OD⊥EF,
∴∠BOC=90°,∠DOF=90°,
∴∠BOF=∠DOC,
在△BOF和△COD中,
$\left\{\begin{array}{l}{OB=OC}\\{∠BOF=∠COD}\\{OF=OD}\end{array}\right.$,
∴△BOF≌△COD,
∴BF=CD,∠OBF=∠OCD,
∴∠CHB=∠COB=90°,
∴BF⊥CD.
点评 本题考查了等腰直角三角形的性质、求得三角形的性质与判定定理,解决本题的关键是利用等腰三角形的性质,证明三角形全等.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
20.关于x的一元二次方程x2-(2m-1)x+m2-1=0的两实数根为x1,x2,且x12+x22=3,则m的值是( )
| A. | 0 | B. | 0或2 | C. | 2 | D. | 0或-2 |
15.下列四个式子中,是一元一次方程的是( )
| A. | 3y+5 | B. | y-1=0 | C. | x-y=5 | D. | y2+y=1 |
16. 已知:△ABC中,AB的垂直平分线分别交AC、AB于点D、E.AC=5,BC=3,AB=7.则△BCD的周长( )
已知:△ABC中,AB的垂直平分线分别交AC、AB于点D、E.AC=5,BC=3,AB=7.则△BCD的周长( )
 已知:△ABC中,AB的垂直平分线分别交AC、AB于点D、E.AC=5,BC=3,AB=7.则△BCD的周长( )
已知:△ABC中,AB的垂直平分线分别交AC、AB于点D、E.AC=5,BC=3,AB=7.则△BCD的周长( )| A. | 7.5 | B. | 8 | C. | 10 | D. | 12 |
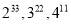 ; ____________________
; ____________________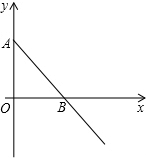 如图,在平面直角坐标系中,直线AB与y轴的正半轴交于点A,与x轴交于点B(2,0),三角形△ABO的面积为2.点Q的坐标是(4,0).动点P从点O出发,以每秒1个单位长度的速度在射线OB上运动,过P作PM⊥x轴交直线AB于M.
如图,在平面直角坐标系中,直线AB与y轴的正半轴交于点A,与x轴交于点B(2,0),三角形△ABO的面积为2.点Q的坐标是(4,0).动点P从点O出发,以每秒1个单位长度的速度在射线OB上运动,过P作PM⊥x轴交直线AB于M.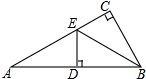 如图,在△ABC中,∠C=90°,BE平分∠ABC,ED⊥AB于D,若AC=6cm,求AE+DE的长度.
如图,在△ABC中,∠C=90°,BE平分∠ABC,ED⊥AB于D,若AC=6cm,求AE+DE的长度.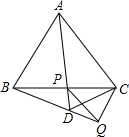 已知△ABC是边长为5的等边三角形.
已知△ABC是边长为5的等边三角形.