题目内容
6.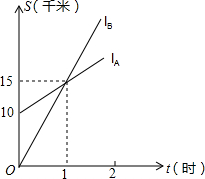 如图,lA、lB分别表示小明步行与小刚骑车在同一条路上行驶的路程S与时间t之间的关系.
如图,lA、lB分别表示小明步行与小刚骑车在同一条路上行驶的路程S与时间t之间的关系.(1)小刚出发时与小明相距10千米.
(2)小刚出发后1 小时追上小明.
(3)分别求出小明行走的路程S1和小刚行走的路程S2与时间t的函数关系式.
分析 (1)利用函数图象直接得出答案;
(2)利用函数图象直接得出答案;
(3)分别利用待定系数法求一次函数解析式和正比例函数解析式即可.
解答 解:(1)由图象可得:B出发时与A相距10千米.
故答案为:10;
(2)由图象可得出:B出发后1小时与A相遇.
故答案为:1;
(3)设S1=kt+b,将(0,10),(1,15)代入得出:
$\left\{\begin{array}{l}{k+b=15}\\{b=10}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=5}\\{b=10}\end{array}\right.$
故:S1=5t+10;
设S2=at,将(1,15)代入得出:
a=15,
则 S2=15t.
点评 此题主要考查了一次函数的应用,正确利用待定系数法求出一次函数解析式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列不等式成立的是( )
| A. | sin30°<sin45°<sin60° | B. | cos60°>cos45°>cos30° | ||
| C. | tan60°<tan45°<tan30° | D. | cot30°<cot45°<cot60° |
11.关于x的一元二次方程x2+x+a-1=0的一个根是0,则a值为( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | $\frac{1}{2}$ |
 如图,△ACE,△ABF都是等腰直角三角形.∠BAF=∠CAE=90°.那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合.
如图,△ACE,△ABF都是等腰直角三角形.∠BAF=∠CAE=90°.那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合.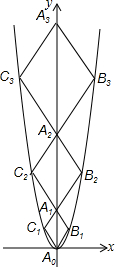 二次函数y=$\sqrt{3}$x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数位于第一象限的图象上,点C1,C2,C3,…,Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3,…,四边形An-1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An-1BnAn=120°.则A1的坐标为(0,2$\sqrt{3}$);菱形An-1BnAnCn的边长为2n.
二次函数y=$\sqrt{3}$x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数位于第一象限的图象上,点C1,C2,C3,…,Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3,…,四边形An-1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An-1BnAn=120°.则A1的坐标为(0,2$\sqrt{3}$);菱形An-1BnAnCn的边长为2n.