Question

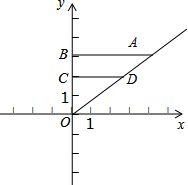在直角坐标中，点A坐标为（4，3），点D为OA上一点，OD=

5

2

，AB⊥y轴于点B，DC⊥y轴于点C．
（1）求点D的坐标；
（2）求四边形ABCD的面积．

Answer 1

考点：勾股定理,坐标与图形性质,梯形

专题：

分析：（1）根据题意，推出△ODC∽△OAB，即可求出D点的坐标；
（2）根据（1）的结论，可知C为OB的中点，即可推出BC的长度，依据A、D两点的横坐标，可知CD、AB的长度，就可以求出四边形ABCD的面积．

解答：解：（1）∵点A的坐标为（4，3），
∴OA=5
∵OD=

5

2

，
∴

OD

OA

=

1

2

，
∵AB⊥y轴，DC⊥y轴，
∴AB∥CD
∴△ODC∽△OAB，
∴

OC

OB

=

CD

AB

=

1

2

，
∴OC=

3

2

，CD=2，
∴点D的坐标为（2，

3

2

）；

（2）∵AB∥CD且AB⊥BC，
∴四边形ABCD是直角梯形，
∵AB=4，CD=2，BC=

3

2

，
∴S梯形ABCD=

1

2

×

3

2

×（4+2）=

9

2

．

点评：本题主要考查相似三角形的判定和性质、梯形的面积公式，解题关键在于求得D点的坐标．