题目内容
15.解不等式组:$\left\{\begin{array}{l}{3x+4<5x-2}\\{x>\frac{1}{3}x-\frac{4}{3}}\end{array}\right.$.分析 分别求出每一个不等式的解集,再确定出不等式组的解集.
解答 解:$\left\{\begin{array}{l}{3x+4<5x-2①}\\{x>\frac{1}{3}x-\frac{4}{3}②}\end{array}\right.$,
由①得,x>3,
由②得,x>-2,
∴不等式组的解集为x>3.
点评 此题是解一元一次不等式组,解本题的关键是准确求出每一个不等式的解集.

练习册系列答案
相关题目
10.已知一个直角三角形的两边长分别为1和2,则第三边长是( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$或$\sqrt{5}$ |
5.有一组数据:6,6,5,4,3,它们的中位数和众数分别是( )
| A. | 3,5 | B. | 4,5 | C. | 5,5 | D. | 5,6 |
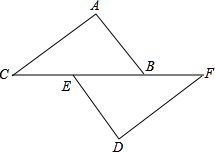 如图,已知点B,E,C,F在一条直线上,BF=CE,AC=DF,现要使△ABC与△DEF全等,需要添加的一个条件是∠ACB=∠DFE或AB=DE.
如图,已知点B,E,C,F在一条直线上,BF=CE,AC=DF,现要使△ABC与△DEF全等,需要添加的一个条件是∠ACB=∠DFE或AB=DE.