题目内容
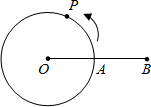 如图,点A是半径为12cm的⊙O上的定点,动点P从A出发,以2π cm/s的速度沿圆周逆时针运动,当点P回到点A立即停止运动,点B是OA延长线上的一点,AB=OA,若点P运动的时间为t.
如图,点A是半径为12cm的⊙O上的定点,动点P从A出发,以2π cm/s的速度沿圆周逆时针运动,当点P回到点A立即停止运动,点B是OA延长线上的一点,AB=OA,若点P运动的时间为t.(1)如果∠POA=90°,求t的值;
(2)当BP与⊙O相切时,求t的值.
(3)当t为何值时,△POB为锐角三角形?钝角三角形?(只要写出结果,不要求写过程)
分析:(1)当∠POA=90°时,点P运动的路程为⊙O周长的
或
,所以分两种情况进行分析;
(2)根据题意画出图形再解答,分两种情况分别计算弧长后求解;
(3)结合(2)的解题过程和图形直接回答.
| 1 |
| 4 |
| 3 |
| 4 |
(2)根据题意画出图形再解答,分两种情况分别计算弧长后求解;
(3)结合(2)的解题过程和图形直接回答.
解答: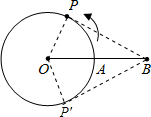 解:(1)当∠POA=90°时,点P运动的路程为⊙O周长的
解:(1)当∠POA=90°时,点P运动的路程为⊙O周长的
或
,
设点P运动的时间为ts;
当点P运动的路程为⊙O周长的
时,2π•t=
•2π•12,
解得t=3;
当点P运动的路程为⊙O周长的
时,2π•t=
•2π•12,
解得t=9;
∴当∠POA=90°时,点P运动的时间为3s或9s;
(2)解:如图,连接OP,则OP=12cm,OB=24cm.
在Rt△OPB中,OP=
OB,故∠BOP=60°.
的长l=
=4π,
故当t=
=2s时,BP与⊙O相切;
同理当P运动到P′时,∠AOP′=360°-60°=300°.优弧
=
=20π,
故当t=
=10s时,BP与⊙O相切.
∴当点P运动的时间为2s或10s时,BP与⊙O相切;
(3)由(1)、(2)知,点P运动的时间为3s或9s或2s或10s时,△POB为直角三角形.
如图,当0<t<2、3<t<6、6<t<9、10<t<12时,△POB为钝角三角形;
当2<t<3、9<t<10△POB为锐角三角形.
 解:(1)当∠POA=90°时,点P运动的路程为⊙O周长的
解:(1)当∠POA=90°时,点P运动的路程为⊙O周长的| 1 |
| 4 |
| 3 |
| 4 |
设点P运动的时间为ts;
当点P运动的路程为⊙O周长的
| 1 |
| 4 |
| 1 |
| 4 |
解得t=3;
当点P运动的路程为⊙O周长的
| 3 |
| 4 |
| 3 |
| 4 |
解得t=9;
∴当∠POA=90°时,点P运动的时间为3s或9s;
(2)解:如图,连接OP,则OP=12cm,OB=24cm.
在Rt△OPB中,OP=
| 1 |
| 2 |
 |
| AP |
| 60π×12 |
| 180 |

故当t=
| 4π |
| 2π |
同理当P运动到P′时,∠AOP′=360°-60°=300°.优弧
 |
| APP′ |
| 300π×12 |
| 180 |
故当t=
| 20π |
| 2π |
∴当点P运动的时间为2s或10s时,BP与⊙O相切;
(3)由(1)、(2)知,点P运动的时间为3s或9s或2s或10s时,△POB为直角三角形.
如图,当0<t<2、3<t<6、6<t<9、10<t<12时,△POB为钝角三角形;
当2<t<3、9<t<10△POB为锐角三角形.
点评:本本题考查的是圆的综合题.其中涉及到了钝角三角形与锐角三角形的判定的,切线的性质及弧长公式,解答(2)题时要注意过圆外一点有两条直线与圆相切,不要漏解.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
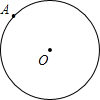 如图,点A是半径为
如图,点A是半径为| 8 |
| π |
A、当P,Q两点运动到1秒时,弦长PQ=
| ||||
B、当点P第一次回到出发点A时所用时间为
| ||||
| C、当P,Q两点从开始运动到第一次成为最大弦时,所用的时间为2秒 | ||||
D、当P,Q两点从开始运动到第一次成为最大弦时,过点A作⊙O的切线与PQ的延长交于M,则MA长为
|
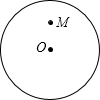 如图,点M是半径为5的⊙O内一点,且OM=3,在过点M的所有⊙O的弦中,弦长为偶数的弦的条数为( )
如图,点M是半径为5的⊙O内一点,且OM=3,在过点M的所有⊙O的弦中,弦长为偶数的弦的条数为( )| A、2 | B、3 | C、4 | D、5 |
 点作⊙O的割线PAB(PB>PA).设PA=x,PB=y.
点作⊙O的割线PAB(PB>PA).设PA=x,PB=y. 8、如图,点P是半径为5的⊙O内一点,且OP=3.过点P任作一条弦AB,则弦AB的长不可能为( )
8、如图,点P是半径为5的⊙O内一点,且OP=3.过点P任作一条弦AB,则弦AB的长不可能为( )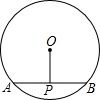 如图,点P是半径为5的⊙O内一点,且弦AB⊥OP,OP=3,则弦AB长是
如图,点P是半径为5的⊙O内一点,且弦AB⊥OP,OP=3,则弦AB长是