题目内容
17.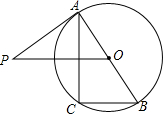 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连结AC.求证:△ABC∽△POA.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连结AC.求证:△ABC∽△POA.
分析 由BC∥OP可得∠AOP=∠B,根据直径所对的圆周角为直角可知∠C=90°,再根据切线的性质知∠OAP=90°,从而可证△ABC∽△POA.
解答 证明:∵BC∥OP,
∴∠AOP=∠B,
∵AB是直径,
∴∠C=90°,
∵PA是⊙O的切线,切点为A,
∴∠OAP=90°,
∴∠C=∠OAP,
∴△ABC∽△POA.
点评 本题主要考查相似三角形的性质与判定、切线的性质等知识,掌握相似三角形的判定定理是解题的关键.

练习册系列答案
相关题目
8. 如图,点O在直线AB上,∠COD=90°,若∠COA=36°,则∠DOB的度数是( )
如图,点O在直线AB上,∠COD=90°,若∠COA=36°,则∠DOB的度数是( )
 如图,点O在直线AB上,∠COD=90°,若∠COA=36°,则∠DOB的度数是( )
如图,点O在直线AB上,∠COD=90°,若∠COA=36°,则∠DOB的度数是( )| A. | 36° | B. | 54° | C. | 64° | D. | 72° |
5.在科学计算器上按顺序按3,8,×,1,5,+,3,2,=,最后屏幕上显示( )
| A. | 686 | B. | 602 | C. | 582 | D. | 502 |
9. 关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
 关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )| A. | -6 | B. | -12 | C. | 6 | D. | 12 |
7. 若实数a,b,c在数轴上对应点的位置如图所示,则下列不等式不成立的是( )
若实数a,b,c在数轴上对应点的位置如图所示,则下列不等式不成立的是( )
 若实数a,b,c在数轴上对应点的位置如图所示,则下列不等式不成立的是( )
若实数a,b,c在数轴上对应点的位置如图所示,则下列不等式不成立的是( )| A. | b>a | B. | ab>0 | C. | a+b<0 | D. | c+a>0 |
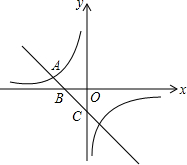 如图,反比例函数y=$\frac{k}{x}$图象与一次函数y=-x-1图象的一个交点为A(-2,a).
如图,反比例函数y=$\frac{k}{x}$图象与一次函数y=-x-1图象的一个交点为A(-2,a).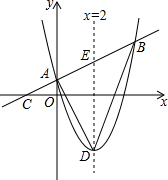 如图,对称轴为直线x=2的抛物线y=x2+mx+1的顶点为D,与y轴相交于点A,过点A作AD的垂线交x轴于点C,交抛物线的对称轴于点E,且与抛物线的另一个交点为B.
如图,对称轴为直线x=2的抛物线y=x2+mx+1的顶点为D,与y轴相交于点A,过点A作AD的垂线交x轴于点C,交抛物线的对称轴于点E,且与抛物线的另一个交点为B.