题目内容
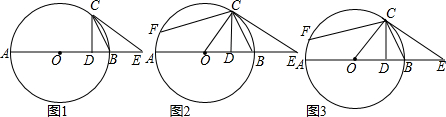
11. 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论:
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论:①当x=3时,y=0;
②3a+b>0;
③-1≤a≤-$\frac{2}{3}$;
④$\frac{8}{3}$≤n≤4.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由抛物线的顶点坐标的横坐标可得出抛物线的对称轴为x=1,结合抛物线的对称性及点A的坐标,可得出点B的坐标,由点B的坐标即可断定①正确;②由抛物线的开口向下可得出a<0,结合抛物线对称轴为x=-$\frac{b}{2a}$=1,可得出b=-2a,将b=-2a代入3a+b中,结合a<0即可得出②不正确;③由抛物线与y轴的交点的范围可得出c的取值范围,将(-1,0)代入抛物线解析式中,再结合b=-2a即可得出a的取值范围,从而断定③正确;④结合抛物线的顶点坐标的纵坐标为$\frac{4ac-{b}^{2}}{4a}$,结合a的取值范围以及c的取值范围即可得出n的范围,从而断定④正确.综上所述,即可得出结论.
解答 解:①由抛物线的对称性可知:
抛物线与x轴的另一交点横坐标为1×2-(-1)=3,
即点B的坐标为(3,0),
∴当x=3时,y=0,①正确;
②∵抛物线开口向下,
∴a<0.
∵抛物线的顶点坐标为(1,n),
∴抛物线的对称轴为x=-$\frac{b}{2a}$=1,
∴b=-2a,
3a+b=a<0,②不正确;
③∵抛物线与y轴的交点在(0,2)、(0,3)之间(包含端点),
∴2≤c≤3.
令x=-1,则有a-b+c=0,
又∵b=-2a,
∴3a=-c,即-3≤3a≤-2,
解得:-1≤a≤-$\frac{2}{3}$,③正确;
④∵抛物线的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),
∴n=$\frac{4ac-{b}^{2}}{4a}$=c-$\frac{{b}^{2}}{4a}$,
又∵b=-2a,2≤c≤3,-1≤a≤-$\frac{2}{3}$,
∴n=c-a,$\frac{8}{3}$≤n≤4,④正确.
综上可知:正确的结论为①③④.
故选C.
点评 本题考查了二次函数图象与系数的关系,解题的关键是结合图象以及给定条件逐个分析4条结论.本题属于基础题,难度不大,解决该题型题目时,利用二次函数的系数表示出来抛物线的顶点坐标是关键.

| A. | 较大的会场设计成阶梯状 | |
| B. | 城市许多路口设计得都十分宽阔 | |
| C. | 城市设计了许多高层住宅 | |
| D. | 汽车上,司机前的玻璃窗面积设计的尽量大 |
| A. | 3a2-a2=3 | B. | a2•a4=a8 | C. | a8÷a2=a5 | D. | (a3)2=a6 |
| A. | a3 | B. | a2 | C. | a9 | D. | a-3 |
| A. | x3•x2=x4 | B. | x(x-2)=-2x+x2 | C. | (x+y)(x-y)=x2+y2 | D. | 3x3y2÷xy2=3x4 |
| A. | 2x+1=2x2 | B. | x2•x3=x5 | C. | (x2)3=x5 | D. | (2x)3=2x3 |
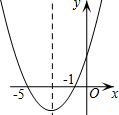 如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2-4ac>0;④a+b+c<0;⑤对于图象上的两点(-6,m )、(1,n),有m<n.其中正确信息的个数有( )
如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2-4ac>0;④a+b+c<0;⑤对于图象上的两点(-6,m )、(1,n),有m<n.其中正确信息的个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | b5•b5=2b5 | B. | (an-1)3=a3n-1 | C. | a+2a2=3a3 | D. | (a-b)5(b-a)4=(a-b)9 |