��Ŀ����
��ͼ��������ABCD�ı�BC�ڵ���ֱ��������PQR�ĵױ�QR�ϣ�������������A��D�ֱ���PQ��PR�ϣ���PA��AQ����������
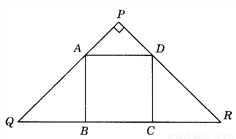
A. 1��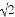 B. 1��2 C. 1��3 D. 2��3
B. 1��2 C. 1��3 D. 2��3
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ��������ABCD�ı�BC�ڵ���ֱ��������PQR�ĵױ�QR�ϣ�������������A��D�ֱ���PQ��PR�ϣ���PA��AQ����������

A. 1��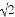 B. 1��2 C. 1��3 D. 2��3
B. 1��2 C. 1��3 D. 2��3