题目内容
1.方程x2-|2x-1|-4=0,求满足该方程的所有根之和为( )| A. | 0 | B. | 2 | C. | $2+\sqrt{6}$ | D. | 2-$\sqrt{6}$ |
分析 因为题目中带有绝对值符号,所以必须分两种情况进行讨论,去掉绝对值符号,得到两个一元二次方程,求出方程的根,不在讨论范围内的根要舍去.
解答 解:①当2x-1≥0时,即x≥$\frac{1}{2}$,原方程化为:x2-2x-3=0,(x-3)(x+1)=0,
x1=3,x2=-1,
∵-1<$\frac{1}{2}$,
∴x2=-1(舍去)
∴x=3;
②当2x-1<0,即x<$\frac{1}{2}$时,原方程化为:x2+2x-5=0,(x+1)2=6,
x+1=±$\sqrt{6}$,x1=-1+$\sqrt{6}$,x2=-1-$\sqrt{6}$
∵-1+$\sqrt{6}$>$\frac{1}{2}$,∴x1=-1+$\sqrt{6}$(舍去)
∴x=-1-$\sqrt{6}$.
则3+(-1-$\sqrt{6}$)=2-$\sqrt{6}$.
故选:D.
点评 本题考查的是解一元二次方程,由于带有绝对值符号,必须对题目进行讨论,对不在讨论范围内的根要舍去.

练习册系列答案
相关题目
12.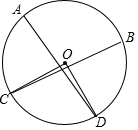 如图,已知在圆O中,劣弧AB的长度是周长的$\frac{1}{3}$,C与D在优弧AB上运动,连接AD与BC交于E点,当∠AEC=∠COD时,则∠COD=( )
如图,已知在圆O中,劣弧AB的长度是周长的$\frac{1}{3}$,C与D在优弧AB上运动,连接AD与BC交于E点,当∠AEC=∠COD时,则∠COD=( )
 如图,已知在圆O中,劣弧AB的长度是周长的$\frac{1}{3}$,C与D在优弧AB上运动,连接AD与BC交于E点,当∠AEC=∠COD时,则∠COD=( )
如图,已知在圆O中,劣弧AB的长度是周长的$\frac{1}{3}$,C与D在优弧AB上运动,连接AD与BC交于E点,当∠AEC=∠COD时,则∠COD=( )| A. | 90° | B. | 45° | C. | 80° | D. | 70° |
6.中国超级计算机神威“太湖之光”,峰值计算速度达每秒12.5亿亿次,为世界首台每秒超10亿亿次运算的计算机,用科学记数法表示12.5亿亿次/秒为( )亿次/秒.
| A. | 12.5×108 | B. | 12.5×109 | C. | 1.25×108 | D. | 1.25×109 |
10.如果x2-2(m-1)x+9是一个完全平方式,则m的取值是( )
| A. | -5 | B. | -4 | C. | -5或7 | D. | -2或4 |
11.2017年5月18日,我国宣布在南海神狐海域成功试采可燃冰,成为世界上首个在海域连续稳定产气的国家.据粗略估计,仅南海北部陆坡的可燃冰资源就达到186亿吨油当量,达到我国陆上石油资源总量的50% .数据186亿吨用科学记数法可表示为( )
.数据186亿吨用科学记数法可表示为( )
 .数据186亿吨用科学记数法可表示为( )
.数据186亿吨用科学记数法可表示为( )| A. | 186×108吨 | B. | 18.6×109吨 | C. | 1.86×1010吨 | D. | 0.186×1011吨 |
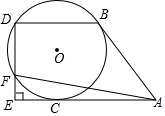 如图,AB,Ac与⊙O相切于点B,C,BD∥AC交⊙O于点D,DE⊥AC交AC的延长线于E,交⊙O于点F,∠BAF=45°.
如图,AB,Ac与⊙O相切于点B,C,BD∥AC交⊙O于点D,DE⊥AC交AC的延长线于E,交⊙O于点F,∠BAF=45°.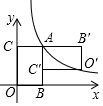 如图,矩形ABOC的顶点O在坐标原点,顶点B,C分别在x,y轴的正半轴上,顶点A在反比例函数y=$\frac{k}{x}$(k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针方向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则$\frac{OB}{OC}$的值是$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABOC的顶点O在坐标原点,顶点B,C分别在x,y轴的正半轴上,顶点A在反比例函数y=$\frac{k}{x}$(k为常数,k>0,x>0)的图象上,将矩形ABOC绕点A按逆时针方向旋转90°得到矩形AB′O′C′,若点O的对应点O′恰好落在此反比例函数图象上,则$\frac{OB}{OC}$的值是$\frac{\sqrt{5}-1}{2}$.